SoK: Cryptographic Neural-Network Computation

Abstract

We studied \(53\) privacy-preserving neural-network papers in 2016-2022 based on cryptography (without trusted processors or differential privacy), \(16\) of which only use homomorphic encryption, \(19\) use secure computation for inference, and \(18\) use non-colluding servers (among which \(12\) support training), solving a wide variety of research problems. We dissect their cryptographic techniques and “love-hate relationships” with machine learning alongside a genealogy highlighting noteworthy developments. We also re-evaluate the state of the art under WAN. We hope this can serve as a go-to guide connecting different experts in related fields.

Introduction

Secure machine-learning (ML) computation, specifically privacy-preserving neural networks (PPNN), has attracted much attention for their broad applicability in often privacy-sensitive scenarios. Model owners who provide inference services or powerful cloud platforms that provide training services might not always be trusted to ensure the data privacy of the inference query or the training data. Cryptographic techniques come in handy in realizing four privacy services (Table 1) – oblivious inference, outsourced inference, outsourced training (by one data owner), and private training (for multiple data owners).

Oblivious Inference. Many inference applications involve sensitive data in queries.

Model owners could give the neural network (NN) to queriers for local evaluation, but they often see the model as a valuable intellectual property (Tramèr et al. 2016). Leaking models also paves the way for attacks (Goodfellow, Shlens, and Szegedy 2015; Papernot et al. 2018; Riazi, Rouhani, and Koushanfar 2019).

In oblivious inference, a querier can learn the inference result (and what is inferrable from it) in a secure two-party computation manner over the query and the model parameters acquired from the training.

Outsourced Inference/Training. Model owners may not have in-house facilities for running inference services. With secure outsourced inference, untrusted third parties can be delegated to answer queries without knowing the model, i.e., it is a threat that any server is curious about the model too.

Likewise, the data owner may desire secure outsourced training. (Frameworks for outsourced training mostly support outsourced inference because handling queries is a sub-routine of NN training.)

Private Training. Multiple mutually distrustful data owners can collectively train an NN with privacy using interactive protocols. Typically, the job can be done by servers that none of them trust for data privacy.

We use the term private training for multiple owners, which covers outsourced training (for one data owner).

Early Works focused on the less complex task of inference. Barni, Orlandi, and Piva (Barni, Orlandi, and Piva 2006; Orlandi, Piva, and Barni 2007) process model and query by (additive) homomorphic encryption (HE) for linear NN computations and garbled circuits (Yao 1986) and HE (with polynomial approximation) for non-linear ones.

Sadeghi and Schneider (Sadeghi and Schneider 2008) rely on secure universal-circuit evaluation (Yao 1986; Goldreich, Micali, and Wigderson 1987) solely. It was 2006-08 when NN did not (re-)gain its popularity, and fully-HE (Gentry 2009) and leveled-HE (LHE) were not available.

In 2016, a purely LHE-based oblivious inference solution CryptoNets was proposed (Gilad-Bachrach et al. 2016). Shortly afterward, MiniONN (Liu et al. 2017) and SecureML (Mohassel and Zhang 2017) appeared. The former uses secure two-party computation techniques beyond LHE for oblivious inference, while the latter is the first \(2\)-server solution of private training.

Dissecting the Development.

PPNN has then rapidly developed across different disciplines, such as system research, scientific computing, machine learning, and cryptography (or crypto in short), posing a rich set of challenging problems requiring quite a few different skill sets to tackle. We systematize \(53\) frameworks born in these \(8\) years, microscopically explore their different technical contributions, and categorize them by their problem settings and major approaches, summarized in our Summary of all Frameworks.

We call NN software frameworks (e.g., PyTorch) by libraries instead.

Our genealogy sorts out the branches in the literature for a clear genealogy and easy identification of research gaps/opportunities.

Prior surveys focus on HE-based works (Tanuwidjaja, Choi, and Kim 2019) or an overlapping subset of \({\leq}13\) frameworks (Riazi, Rouhani, and Koushanfar 2019; Azraoui et al. 2019) without aiming for a clear lineage of ideas.

Easier Comparisons. This SoK also explains the commonly-used benchmarks and sheds light on how to gauge a framework, which to use for a given setting/goal, and which frameworks to compare with, e.g., to avoid unfair comparison between one assuming non-colluding servers while the other does not. For the state-of-the-art frameworks assumed to run on LAN, we re-evaluate them on WAN.

We found \(1000\)Mbps is needed for peak performance, but lower bandwidth (\(10 \sim 100\)Mbps) suffices for some of them in non-real-time applications.

Fostering Interdisciplinary Research. Many issues in PPNN may look complicated at first glance to “outsiders.” We explain the challenges and tricks for addressing them. Together with the categorization of contributions in our Summary of all Frameworks, experts of different fields can quickly identify the papers related to their interested (sub-)topics, dive right into the crux, and avoid reinventing the wheel. Finally, we share some outstanding challenges and less-explored open problems at the end of a (sub-)section.

Scope. We focus on purely-crypto-based approaches and exclude those that use a trusted execution environment, e.g., (Ng et al. 2021). As crypto literature, membership inference (Shokri et al. 2017) and model inversion (Fredrikson, Jha, and Ristenpart 2015) are not in our scope; and neither is federated (Q. Yang et al. 2019) or coopetitive learning (Zheng et al. 2019).

Differential privacy (Dwork et al. 2006; Mireshghallah et al. 2020; M. Du, Yue, Chow, and Sun 2023; M. Du, Yue, Chow, Wang, et al. 2023) can serve as defenses.

Finally, we refer to a recent SoK (Cabrero-Holgueras and Pastrana 2021) for longer expositions of the basics, with its scope confined to open-sourced projects and MPC libraries.

Preliminary

Deep Neural Network (DNN)

DNN (or just NN) imitates how biological NNs learn by inferring an underlying model from samples, which can be used for prediction/classification. DNNs simplify the imitation to a stack of linear and non-linear layers \(f_1, \ldots, f_n\); each (except the first input layer) takes the outputs from its previous layer.

More advanced NNs may have multiple paths of layers from inputs to outputs; each may take inputs from more previous layers.

One may see it as a chained function \(\mathsf{NN} = f_n \circ \cdots \circ f_1\) if inputs other than weights are seen as “hardwired” parameters. The description in this section supposes the NNs are for visual tasks.

Linear Layers. Common examples include dense/fully-connected layers (matrix multiplication) and 2D convolution. The weight, i.e., matrices of the model and kernels of the convolution, are learnable parameters that should be kept private. A linear layer outputs \(y_i = \sum_j w_{ij} \cdot x_{ij}\) for weight \(w_{ij}\) and input \(x_{ij}\). Its evaluation can be reduced to dot products.

Common Kinds of Non-Linear Layers:

1. Activation layers apply an activation function to all inputs, e.g., popular \(\mathsf{softmax}\), rectified linear unit \(\mathsf{ReLU}\), \(\mathsf{sigmoid}\), etc.

2. Pooling layers aggregate a window from the \(2\)D-output from their previous layers, e.g., \(\mathsf{maxpool}\), \(\mathsf{meanpool}\), etc.

3. Normalization layers regularize the inputs into a smaller range, e.g., batch normalization (BatchNorm) (Ioffe and Szegedy 2015) maps each pixel to a standard normal distribution across the input batch.

4. The output layer computes the inference output based on all its inputs, e.g., \(\mathsf{softmax}\) or \(\mathsf{argmax}\). For training, it further computes a loss value, judging how good/bad the NN is.

The architecture of an NN specifies the type and dimension of each layer. The dimension of a layer means the size and shape of the inputs and output. Layers may include other specifications, e.g., convolutional and pooling layers take specifications on the shape of the kernels or the pooling windows, respectively.

(Supervised) Training takes a labeled training data set and an architecture and outputs the weights (or learnable parameters) of an NN.

Most NN training adopts stochastic gradient descent (SGD), which updates all weights \(\mathbf{w}\) iteratively over the training data batch-by-batch. During training,

besides computing the outputs, the output layer computes a loss value \(L = \mathcal{L}_\mathbf{w}(y', y)\) respective to \(\mathbf{w}\), where \(y'\) and \(y\) are the labels and the inference outputs of that batch, respectively.

Let \(w_i\) be a weight tensor of the \(i\)-th layer \(f_i\), and \(\Delta w_i\) be its corresponding derivative, the gradient. The weight is updated via \(w_i' = w_i - \alpha \Delta w_i\), where \(\alpha\) is a learning rate to regulate the weight change. With a reasonable \(\alpha\), the loss will gradually decrease, meaning the model can make the right inference according to the training data.

Backward propagation derives \(\Delta w_i\). The derivative of a layer can be computed with that of the next layer recursively via \(\Delta w_i = f'_{i, w}(\Delta x_{i+1}, x_i)\) and \(\Delta x_i = f'_{i, x}(\Delta x_{i+1}, w_i)\), where \(f'_{i, v}\) are functions for computing the derivative for \(v\) in the \(i\)-th layer. Their computation is similar to the layer’s original operations.

So, it can happen recursively and in backward order from \(\Delta w_n = \partial_y L\) in the loss layer to the input layer.

Machine-learning Libraries (e.g., Caffe (Jia et al. 2014), Keras, PyTorch, TensorFlow (Abadi et al. 2016), and Theano) mostly take care of tedious computations of NN inference and training for developers to conveniently realize an NN by just specifying its architecture.

They translate NN specifications into computation graphs, which are then relayed to compilers to generate the machine code. Some PPNN frameworks aim to provide similar convenience.

Common Benchmarks. Oblivious inference aims to reduce the latency, i.e., the time between the initiating query and the return of the result. Another factor, throughput, counts how many queries or training data one can process for a given time. They are jointly affected by the choices of secure protocols, NN architectures, network conditions, and hardware components.

Private training also aims to improve the accuracy of the trained model. It depends on the convergence rate, indicating the needed steps to attain saturated accuracy.

GPUs feature an instruction throughput orders of magnitude higher than CPU when fully utilized: SIMD (single instruction multiple data) performs the same operation across vectorized data simultaneously, while parallelism divides a task for many GPU cores to process. GPUs are mainly optimized for floating-point numbers. They are popular choices for NN computations.

Crypto primitives, however, cannot benefit from GPUs by default as they mostly work on fixed-point numbers. Leveraging GPUs for privacy-preserving NN poses challenges (Tramèr and Boneh 2019; Ng et al. 2021).

Problem Formulation and Computation and Threat Models

We consider an abstract threat model in typical crypto literature.

e.g., the honest party’s hardware and software are not compromised.

Oblivious inference can be cleanly abstracted as the secure two-party computation of \(f(\mathit{model}, \mathit{query}) \rightarrow (\bot, \mathit{result})\). The model owner and the querier are also called the server and the client, respectively. This paper refers to it as server/client or S/C (to avoid confusion with \(2\)PC frameworks using two non-colluding servers on top of two-party computation (\(2\)PC) techniques). In practice, some metadata, such as the dimension of the query as a feature vector, might be considered public knowledge (see the Section on Leakage).

Outsourced inference refers to the same computation, while the \(\mathit{model}\) is outsourced in an encrypted form to a single server or secret-shared (the Section on Secret Sharing) among different non-colluding servers. The querier may or may not interact with servers during the computation. Finally, \(n\)-party private training can be abstracted as the secure multi-party computation of \(f(\langle \mathit{dataset} \rangle_1, \ldots, \langle \mathit{dataset} \rangle_n) \rightarrow (\langle \mathit{model} \rangle_1, \ldots,\langle \mathit{model} \rangle_n)\). Each participant is a non-colluding server, inputs a secret share \(\langle \cdot \rangle\) of the training dataset received from the data contributors, and outputs a secret share \(\langle \cdot \rangle\) of the trained model.

The trained parameters in \(\mathsf{NN}\) are secret protected by secret shares.

Non-colluding assumption means the participants, e.g., helper servers (Rouhani, Riazi, and Koushanfar 2018), will not reveal their secrets to any other parties, e.g., competing cloud servers, prestigious agents, a subset of model owners (in inference), and/or a subset of data contributors (in training).

The number of servers required by existing frameworks ranges from \(2\) to \(4\). An adversary just needs to compromise any two servers for a total break against most of these frameworks covered in this SoK. A \(4\)-party setup is easier to be compromised than a \(3\)-party setup as there is one more server as an attack target. The same applies to \(4\)-/\(3\)- vs. \(2\)-party setups.

Many frameworks adopt offline/online computation to reduce the online latency/throughput.

Consider oblivious inference; in the offline phase, one can prepare, probably in batch, pre-computed results without knowing the query, using techniques that might be heavier than those in online computation. In the online phase, where the query is known, the pre-computed results can speed up the online computation.

Cryptographic Primitives

Secure Multi-Party Computation (MPC)

allows mutually distrustful parties to jointly compute a known function over their respective secret inputs via interactions. The computation results are often secret-shared in some forms among the parties. We refer to the MPC for \(n\) parties by \(n\)PC (e.g., \(4\)PC). We also refer to frameworks with non-colluding servers by MPC frameworks.

\((t, n)\) Secret Sharing (SS)

SS distributes a secret \(x\) into shares \(\{\langle x \rangle_i\}\) for \(n\) parties; \(x\) can be recovered from any \(t \geq n\) shares, e.g., \(\langle x \rangle_0 \in \mathbb{Z}_p\) and \(\langle x \rangle_1 = x - \langle x \rangle_0 \bmod{p}\) are \((2, 2)\) additive SS of \(x \in \mathbb{Z}_p\). When \(p \gg 2\), we also call them arithmetic SS. Addition and constant multiplication can be done locally.

Multiplication over SSs \(\langle x \cdot y \rangle\) from \(\langle x \rangle, \langle y \rangle\) can be done using Beaver’s trick (Beaver 1991), which requires both parties to have prepared offline (via HE, oblivious transfer, or a non-colluding server) additive SS of \(u, v, z\) (Beaver triplets), where \(z = u \cdot v\).

Boolean SS \((2, 2)\)-shares a bit-string via bit-wise exclusive OR (\(\mathsf{XOR}\)) over \(\mathbb{Z}_2\).

GMW protocol of Goldreich et al. (Goldreich, Micali, and Wigderson 1987) can evaluate logic gates (e.g., \(\mathsf{AND}\), \(\mathsf{XOR}\)), simple circuits (e.g., \(\mathsf{CMP}\) for comparison), and a composed circuit over them. To save communication rounds, we may run GMW in parallel for some gates, but its runtime is still linear in the circuit depth.

Yao’s Garbled Circuit (GC)

GC (Yao 1986) also supports oblivious \(2\)PC circuit evaluation over “encrypted” truth tables of gates, with decryption keys named Yao’s shares. GC only takes constant communication rounds.

Moreover, the encrypted truth table can be sent in the offline phase. In the online phase, the garbler only obliviously sends the evaluator the shares for input. In contrast, GMW requires interaction for each \(\mathsf{AND}\) gate. Thus, GC is thus a better choice than GMW for \(2\)PC (Demmler, Schneider, and Zohner 2015).

Oblivious Transfer (OT)

allows the receiver to pick the \(i\)-th item obliviously (hiding \(i\)) from the sender’s table of items \(A_1, \ldots, A_n\), i.e., it realizes \(2\)PC \(f(\{A_j\}, i) \rightarrow (\bot, A_i)\). In OT extension (Ishai et al. 2003), online crypto operations are solely symmetric-key ones, while public-key operations are shifted offline. OT is a building block for GC and Beaver triplets (Beaver 1991). It also realizes oblivious table lookup with \(O(n)\) communication cost (Dessouky et al. 2017).

With \({\geq} 3\) non-colluding servers, GMW becomes a more popular choice than GC due to the cheap offline phase and the low storage requirement. The third server can cheaply distribute the beaver triplets instead of running the expensive OTs. After the offline phase, GC requires \(E\) to store \({\approx} 256\) bits for each \(\mathsf{AND}\) gate. Yet, GMW only requires the parties to store \(3\) bits in total. It thus reduces the parties’ storage pressure stemming from offline preparation.

Homomorphic Encryption (HE)

supports operations over encrypted messages. Encryption \([x] = \mathsf{Enc}_{\mathsf{pk}}(x)\) of \(x\) can be decrypted by secret key \(\mathsf{sk}\) when \((\mathsf{pk}, \mathsf{sk})\) is a matching key pair.

Additive-HE (AHE), linear-HE, supports additive homomorphism like arithmetic SS.

Leveled-HE (LHE), somewhat-HE, supports a limited number of multiplications corresponding to the depth of an arithmetic circuit. The number is a tunable parameter that affects the ciphertext size and efficiency of the homomorphic operations (the Section on HE optimization).

LHE like BFV-HE (Brakerski 2012; Fan and Vercauteren 2012), BGV-HE (Brakerski, Gentry, and Vaikuntanathan 2014), and CKKS-HE (Cheon et al. 2017) are SIMD-friendly, i.e., a ciphertext has multiple slots, each fits a message in ring \(\mathbb{Z}_p\), and a homomorphic operation (\(\star\), \(\ast\), and \(\circ\)) applies on all slots simultaneously.

Namely,

1. addition: \(\mathsf{Dec}([(x_i)_i] \star [(y_i)_i]) = (x_i + y_i)_i\),

2. plaintext-ciphertext multiplication: \(\mathsf{Dec}((x_i)_i \circ [(y_i)_i]) = (x_i \cdot y_i)_i\), and

3. ciphertext-ciphertext multiplication: \(\mathsf{Dec}([(x_i)_i] \ast [(y_i)_i]) = (x_i \cdot y_i)_i\).

(When the context is obvious, we may replace \(\circ\) and \(\ast\) by \(\cdot\) and \(\star\) by \(+\).)

For security, they introduce noises to ciphertexts. Fresh encryption starts with very little noise. Noises accumulate upon evaluating \(\star\), \(\ast\), and \(\circ\). If they exceed the noise quota, decryption will fail.

The quota implicitly defines the number of \(\star\), \(\ast\), and \(\circ\) allowed to take. Yet, one can ask the secret key holder to help “denoise” the ciphertext by adding an additive mask (via \(\star\)) without leaking the encrypted message (see the Section on efficient HE).

Two SIMD Layouts. Consider the central part of a photo is of interest; one ciphertext thus stores the same part of many photos. Such kind of batch-query processing via SIMD is relevant only when the client always has a batch of queries. An alternative usage is to handle one single (feature-vector) query at a time, but with its features spread across SIMD slots of a ciphertext.

One may want to homomorphically evaluate over multiple slots of a query (e.g., for a dot product). A homomorphic rotation over the encrypted query is required. Rotation is more computationally expensive than plaintext-ciphertext multiplication and addition. It also increases the noise additively (Brakerski, Gentry, and Vaikuntanathan 2014; D. J. Wu and Haven 2012).

TFHE (Chillotti et al. 2020) is torus-based fully-HE (FHE) with much faster bootstrap procedures but slower addition/multiplication than BFV-HE and BGV-HE. TFHE is mainly used to evaluate binary gates (Bourse et al. 2018; Sanyal et al. 2018; Lou and Jiang 2019) with very little communication cost (proportional to the input size) when compared to GC/GMW (the whole circuit size), but it takes a longer computation time.

BFV-HE, BGV-HE, and TFHE are all based on ring-LWE. A ciphertext under one scheme can be switched to that of another with the message inside unchanged (Boura et al. 2019).

Microsoft SEAL implements BFV-HE and CKKS-HE. HElib implements BGV-HE. TFHE library is on GitHub.

General Comparison of the Gadgets.

Arithmetic SS operations can be as cheap as a few CPU instructions, but each multiplication takes a communication round.

HE could be a better choice in general in a high-latency network as no communication is needed in between. This motivates pure-HE frameworks (the Sections on pure-LHE frameworks and on TFHE frameworks) and differentiates them from the rest.

LHE and arithmetic SS are born to handle linear layers. Boolean/circuit-based primitives, including TFHE, boolean SS, and Yao’s shares, support arbitrary functions, including non-linear ones. This motivates the mixed framework.

Arithmetic SS, boolean SS, and Yao’s shares (A/B/Y) can be converted to each other with a few communication rounds (except Y to B, which is free) such that one can use mixed-protocol computation with the most-fit form for each kind of computation. ABY (Demmler, Schneider, and Zohner 2015) is proposed for this purpose.

This leads to interesting interbreeds in mixed and MPC frameworks (the Section on MPC).

Struggles in Fixed-Points and Limited Bitwidth.

Most crypto primitives operate over \(\mathbb{Z}_p\) for a large prime \(p\), which we call fixed-points, while NN runs over floating-point numbers, which we call floats.

A float \(x_f\) can be quantized as fixed-point \(x_Q = \lfloor x_f \cdot P_x \rceil\) for the scaling factor \(P_x\). We can then avoid overflow in, say, dot product by computing over fixed points. The resulting fixed \(y_Q\) can then be dequantized by \(y_f = y_Q / P_y\).

Bitwidth is the number of bits needed to represent the operands, which is logarithmic in the largest magnitude.

To fully emulate single-precision floats, one may need \(256\)-bit fixed points. More bitwidth means more transferred bytes, CPU/GPU instructions, larger circuits for GMW/GC, and collectively much higher communication and computation costs.

As a rather fundamental issue, different classes of frameworks tackle a slightly different form of it in their own ways.

Systematizing Machine learning \(\times\) Cryptology

Crypto operations usually incur high overhead and tend to attain a lower accuracy for operating over fixed-points (e.g., see the Section on mixed bitwidth).

We highlight the initial struggles and some milestones. A query on MNIST takes CryptoNets (Gilad-Bachrach et al. 2016) \(300\)s. Two years later, Gazelle (Juvekar, Vaikuntanathan, and Chandrakasan 2018) takes only \(0.03\)s. Building upon the success of mixed frameworks, GForce (Ng and Chow 2021) can process a query on CIFAR-10, a harder dataset, within \(0.3\)s online latency using the popular VGG-16 NN. For the same dataset, Gazelle takes \(3.56\)s with a much smaller, custom NN.

For private training, SecureML (Mohassel and Zhang 2017) over \(2\) non-colluding servers achieves an online training throughput of \({\sim}3.3 \times 10^5\) images/hour on MNIST at \(93\%\) accuracy. Trident (Rachuri and Suresh 2020) over \(4\) servers attained an online throughput \({\sim}1.4\times 10^7\) on the same NN.

To support training on more realistic datasets and popular NNs, CryptGPU (Tan et al. 2021) integrates more advanced ML techniques, e.g., BatchNorm and \(\mathsf{softmax}\), and achieves \(83.7\%\) accuracy on CIFAR-10 with VGG-16 at a \({\sim}4\times 10^4\) online throughput.

PPNN researchers look into the nature of the operations at various levels and their interactions, and tailor-make protocols optimized under constraints due to many reasons, e.g., scientific computation for the traditional setting (of CPU/GPU instead of crypto layers), the ML expectation, and crypto tools. At the layer level, different protocols handle each layer type separately. Such modular designs allow flexibility over many architectures.

Roadmap. Following sections will discuss pure-LHE-based, mixed, and MPC-based frameworks. The Section on depolyment discusses special focuses, which might interest experts outside crypto communities. The Section on benchmarks compares the performance of different frameworks and puts them on the Pareto frontier. The Section on SoTA recommends the state of the arts for specific functions under different settings/assumptions.

Table 1: Privacy Services Supported by Different Paradigms.

Framework Type	Oblivious Inference	Outsourced Inference	Outsourced/Private Training
Pure-LHE	All	Some	None
TFHE-based	All	Some	Some
Pure-GC	All	Some	None
Mixed	All	None	None
MPC-based	All	All	Some

Pure-LHE Frameworks

Pure-LHE frameworks (e.g., CryptoNets (Gilad-Bachrach et al. 2016)) use LHE as the only crypto tool throughout the entire evaluation of oblivious inference.

The client first encrypts the query \(x\) and sends it to the server. For linear layers with weights \(\{w_{ij}\}\), the server computes \([y_i] = \sum_j w_{ij} \cdot [x_{ij}]\) for encrypted layer input \([x_{ij}]\).

Some mixed frameworks also handle linear layers in this way. (We thus defer to the Section on efficient HE for LoLa (Brutzkus, Gilad-Bachrach, and Elisha 2019).) Below, we discuss “BNormCrypt” (Chabanne et al. 2017), CryptoDL (Hesamifard et al. 2018), FasterCryptoNets (Chou et al. 2018), HCNN (Badawi et al. 2021), E2DM (Jiang et al. 2018), and Glyph (Lou et al. 2020) (See the Section on HE compilers/optimizers).

Major Developments for Pure-LHE-based Inference

Non-linear layers pose a challenge to pure-LHE frameworks. They tend to choose specific functions that can be either supported or approximated by polynomials. CryptoNets is a polynomial-network (Livni, Shalev-Shwartz, and Shamir 2014) approach, which uses only squaring \([x] \cdot [x]\) as the activation function. For pooling layers, it only supports \(\mathsf{meanpool}\) by \([y_i] = \sum_j [x_j]\). The client internally maintains the output’s scale after computing each layer (e.g., the output is scaled up by \(d\) for the \(d\)-size window \(\mathsf{meanpool}\)). Eventually, the server sends the output layer’s \([y]\) to the client, who decrypts it (and divides it by the scale) to obtain the query result.

Batch normalization (Ioffe and Szegedy 2015) is an ML trick that helps ensure accuracy by normalizing the range of the inputs since polynomial approximation is only accurate within a small range. “BNormCrypt” (Chabanne et al. 2017) and subsequent works insert BatchNorm layers before activation layers. BatchNorm in inference can be efficiently done with HE ciphertexts since the computation is basically point-wise (plaintext-ciphertext) multiplication and addition. BNormCrypt approximates \(\mathsf{ReLU}\) by \(0.2[x]^2 + 0.5[x] + 0.2\).

Speeding up Multiplication. CryptoDL (Hesamifard et al. 2018) exploits various methods for approximation by low-degree (\(2{\sim}4\)) polynomials, including numerical analysis, Taylor series, and Chebyshev polynomial, since ciphertext-ciphertext multiplication is not cheap.

FasterCryptoNets (Chou et al. 2018) uses power-of-\(2\) coefficients for the polynomials to enable more efficient plaintext-ciphertext multiplication.

It also quantizes the weights of linear layers to power-of-\(2\) for more efficient multiplication.

Pruning sets some weights in a trained NN to \(0\). Pure-LHE frameworks above dedicate each HE ciphertext to a specific entry across all queries in a batch; each entry is then multiplied by the same weight.

These frameworks (e.g., (Chou et al. 2018)) can benefit from pruning by skipping the multiplication of the ciphertext and the zeroed weights, which can skip up to \({>}90\%\) of those.

GPU for HE. HCNN (Badawi et al. 2021) is like CryptoNets. They both use BFV-HE for oblivious inference, but HCNN implements A*FV (Badawi et al. 2018), a variant that better utilizes GPU’s capability.

Outsourced Inference and Training without non-collusion

Notably, HE can support outsourced inference and training without non-colluding assumptions. For example, E2DM (Jiang et al. 2018) uses only cipher-cipher multiplications over private weights. It only demonstrated reasonable performance on NNs with square activation and a few fully-connected layers. Deeper NNs with convolutions require more costly bootstrapping and rotations.

Glyph (Lou et al. 2020) supports outsourced training. It adopts transfer learning to reduce the costly homomorphic operations. It trains many layers close to the input layer of an NN with publicly available data and only uses HE for training the remaining layers with private data.

Glyph does not consider (multi-party) private training as the single secret key owner, effectively the data owner, can decrypt the ciphertexts and acquire all training data. One could use heavyweight multi-key FHE.

We thus ask:

Open Problem 1. How to realize high-throughput and accurate private training without non-colluding assumptions?

Section MPC frameworks will explore such “non-colluding” frameworks.

To sum up, the distinctive feature of the pure-LHE framework is the use of polynomial networks. This begs the question:

Open Problem 2. What positive/negative results can we establish on the sample complexity, expressiveness, and (the practical) training time for networks based on polynomials?

Linvi et al. (Livni, Shalev-Shwartz, and Shamir 2014) provided some results. Understanding more about deep learning still needs more research (C. Zhang et al. 2021). In contrast, Sections \(\mathsf{CMP}\) and non-linear layers explore non-polynomial approaches.

Boolean-Circuit-based Approaches

TFHE-based (Inference) Frameworks

To avoid the higher cost of homomorphic arithmetic operations, an alternative is TFHE (Chillotti et al. 2020), optimized for binary gates. Glyph (Lou et al. 2020) switches between different kinds of ring-LWE-based HE schemes. It uses BGV-HE (Brakerski, Gentry, and Vaikuntanathan 2014) for linear arithmetics and TFHE for de-quantization and non-linear layers.

Binarized neural network (BNN) (Hubara et al. 2016) confines its weights and inputs of linear layers to \(\{-1, 1\}\). It uses \(\mathsf{Sign}(x)=|x|/x\) as the activation function, which is easy to implement in boolean circuits. FHE-DiNN (Bourse et al. 2018) implements BNN on TFHE (Chillotti et al. 2020). It can perform inference on MNIST in \({<}1\)s, but its accuracy is much lower than CryptoNets since it only supports small BNNs. TAPAS (Sanyal et al. 2018) also uses TFHE over BNN. It implements ripple carry adders for linear layers in a recursive manner to avoid errors due to accumulated noise in TFHE.

However, to maintain a reasonable accuracy level, BNN often requires scaling the architecture, i.e., having more outputs in each layer, which enlarges the circuits and cancels out part of the performance gain.

Unlike TAPAS, SHE (Lou and Jiang 2019) supports most common NNs using TFHE. It implements \(\mathsf{ReLU}\) and maxpool as binary circuits. It also uses the power-of-\(2\) idea (Chou et al. 2018), and running shifting circuits in TFHE is efficient.

To efficiently handle the addition after the multiplication, it reduces the circuit size via a mixed-bit-width accumulator, whose size is smaller when the input size is smaller. SHE adopts an intra-layer mixed-bitwidth design for smaller circuits, which also allows the bitwidth to vary across layers to balance the performance and accuracy.

Pure-GC (Inference) Frameworks

The major hurdle of circuit-based approaches is that the circuits (even for linear layers) are bulky and incur a large overhead.

DeepSecure (Rouhani, Riazi, and Koushanfar 2018) uses only GC. It decomposes the input (linear) layer into lower-rank matrices and releases one of them to the client for computing a low-rank projection (of the input). It also uses circuit optimization tools to approximate activation with fewer gates and skip computation for pruned neurons (in a pruned NN).

XONN (Riazi et al. 2019) is dedicated to BNN with pruning applied. It implements XNOR (\(\odot\)) in GC since BNN uses it to count the number of bits after multiplication.

“GarbledNN” (Ball et al. 2019) aims to show that GC can be applied to not only BNN but also “off-the-shelf” NNs, e.g., the TensorFlow model. It uses arithmetic garbling techniques and optimizes for the \(\mathsf{sign}\) function (and \(\mathsf{ReLU}\)).

Namely, it uses a stochastic approach that simplifies comparison gates (\(\mathsf{CMP}\)) in GC by tolerating an error probability \({<}0.1\%\). Yet, this simplified circuit can only work on \(\mathbb{Z}_N\), where \(N\) is a product of many distinct small primes. GarbledNN outperforms DeepSecure, but it still takes \({\sim}15\) minutes to run an NN with only \(6\) linear layers on CIFAR-10. As an approach orthogonal to XONN (for BNN), one might consider combining optimization tricks of both.

Open Problem 3. Tailoring ML techniques for compatibility with cryptographic techniques (vs. the other way round, e.g., HE for linear and GC for non-linear layers, which many earlier PPNN works aim at) is a promising direction. We ask:

“Apart from BNN (and its generalization QNN to be discussed later), any ML techniques can help cryptographic NN?”

Mixed Frameworks for Oblivious Inference

Many oblivious inference frameworks use both HE and SS and/or GC for the best of both worlds, e.g., reduced runtime. We first explore SS-based computation (Delphi, CrypTFlow2, Circa, GForce) before revisiting HE (Gazelle, GALA, “FalconI”).

Offline/Online Share Computation for \(2\)PC (over GPU)

MiniONN (Liu et al. 2017) uses the offline/online trick for computing linear layers \(\langle y_i \rangle = \sum_j w_{ij} \cdot \langle x_{ij} \rangle\) over arithmetic SS and weights \(w_{ij}\) known to the server.

In the offline phase, the client sends \(\{[\langle x_j \rangle_1]\}_j\) encrypting random \(\{\langle x_j \rangle_1\}\) to the server, which then returns \(\sum_j w_j \cdot [\langle x_j \rangle_1] - r'\) for a random \(r'\). The client decrypts it to get \(\langle y \rangle_0 = \sum_j w_j \cdot \langle x_j \rangle_1 - r'\). In the online phase, the client with input \(\{x_j\}_j\) sends \(\{\langle x_j \rangle_0 = x_j - \langle x_j \rangle_1\}_j\) to the server, which then computes \(\langle y \rangle_1 = \sum_j w_j \cdot \langle x_j \rangle_0 + r'\). We call it secure online/offline share computation (SOS). Note that \(\{\langle x_j \rangle_1\}\) can be “reused” for different weights.

SOS-style multiplication of \(\ell\)-bit integers (Mohassel and Zhang 2017; Rathee et al. 2020; Hussain et al. 2021) can also be done by OT. The client picks \(r'_{i}\) and sets \(A_i = (r - r'_i, -r'_i), \forall i \in [0, \ell-1]\) for random \(\langle x \rangle_1 = r\). For each bit \(w_i\) of \(w\) in binary, the server gets \(A_i[w_i]\) via OT and computes \(\langle w \cdot r \rangle_0 = \sum_{i=0}^{\ell-1}{2^iA_i[w_i]} = w\cdot r - \langle y \rangle_1\). The client then computes \(\langle y \rangle_1 = \langle w \cdot r \rangle_1 = \sum_{i=0}^{\ell-1} 2^i r'_i\). (During the online phase, the server computes \(\langle y \rangle_0 = w \cdot \langle x \rangle_0 + \langle w \cdot r \rangle_0\).) Since each OT sends \({\approx}\ell\) bits (after using correlated OTs and packing multiple instances for cost amortization), a multiplication takes \(O(\ell^2)\) bits.

Generalizing to matrices/tensors, the client/server obtains \(\langle Y \rangle_0 = W \otimes R - R'\) or \(\langle Y \rangle_1 = W \otimes (X - R) + R'\), respectively.

For repeated dot products, multiple OTs are needed for varying weights, which takes more communication than using HE.

GPU for SS. In SOS, the client can generate an AHE of an additive mask offline. Once the input arrives, an SS-based protocol is run on the client’s masked input \(\langle X \rangle\). The server in Delphi (Mishra et al. 2020) and GForce (Ng and Chow 2021) can use GPU to compute \(W \otimes \langle X \rangle\) with performance close to plaintext computation.

This observation generalizes SOS to the AHE-to-SOS trick (Ng and Chow 2021) for many compatible operations (e.g., truncation and GForce’s wrap-around protocol below) and non-linear layers. Also, the offline protocol can be optimized separately (see the Section on efficient HE).

Comparison Functions for \(\mathsf{sign}\), \(\mathsf{max}\), and \(\mathsf{ReLU}\)

Non-linear layers in many popular NNs, e.g., VGG and ResNet, only use \(\mathsf{ReLU}\) and \(\mathsf{maxpool}\), which essentially compute \(\langle \mathsf{max}(x, y) \rangle = \mathsf{CMP}_{x \leq_? y}(\langle x \rangle, \langle y \rangle) \cdot \langle y-x \rangle + \langle x \rangle\) (expressed in SS) using a secure comparison protocol \(\mathsf{CMP}\).

\(\mathsf{CMP}\) is also called the derivative of \(\mathsf{ReLU}\) (Wagh, Gupta, and Chandran 2019; Wagh et al. 2021) or bit-extraction for its equivalence to extract the MSB of (\(y - x)\).

\(\mathsf{CMP}\) via GC. \(\mathsf{ReLU}\) and \(\mathsf{maxpool}\) can be implemented by circuits with the comparison gate for \(\mathsf{CMP}\) and multiplexer via the Beaver’s trick after the Yao-to-Arithmetic (Y2A) conversion of ABY (Demmler, Schneider, and Zohner 2015).

MiniONN computes \(\langle \mathsf{ReLU}(x) \rangle = \mathsf{CMP}(\langle x \rangle, 0) \cdot \langle x \rangle\). Gazelle (Juvekar, Vaikuntanathan, and Chandrakasan 2018) computes the entire \(\langle \mathsf{ReLU}(x) \rangle\) in GC. Many later works focus on optimizing the expensive \(\mathsf{CMP}\).

Selective Approximation. The online latency due to linear layers is \({<}0.1\) seconds by using GPU in Delphi. The bottleneck lies in non-linear layers. Delphi computes some \(\mathsf{ReLU}\) layers by GC but others (strategically decided by a planner) by \(x^2\)-approximation. Accuracy is still degraded (Ng and Chow 2021), albeit confined.

Stochastic Approaches. Circa (Ghodsi et al. 2021) simplifies and thus accelerates \(\mathsf{CMP}\) in GC, and truncates its input to suppress its error probability, which is linear in the input’s absolute value.

DGK for GPU. DGK protocol of Damgard et al. (Damgård, Geisler, and Krøigaard 2007) compares two HE-encrypted integers and outputs a result bit. Its naive implementation is slower than GC/GMW’s \(\mathsf{CMP}\). GForce (Ng and Chow 2021) transforms DGK into a bunch of linear operations and fits them with its AHE-to-SOS trick, which outperforms Gazelle (Juvekar, Vaikuntanathan, and Chandrakasan 2018) and Delphi (Mishra et al. 2020), also without any approximation.

An OT-based approach is proposed by CryptFlow2 (Rathee et al. 2020). We discuss a simplified version: For \(x, y \in \mathbb{Z}_{2^\ell}\) respectively held by party \(P_0\) and \(P_1\), \(P_1\) can obliviously select \(\langle x \leq_? y \rangle_1\) from \(P_0\) with \(O(2^\ell)\) communication for bitwidth \(\ell\). To reduce it, CryptFlow2 decomposes \(x\) and \(y\) into \(k\) equal parts, e.g., \(x=x_k||\cdots||x_1\), and uses OT for oblivious selection over each pair of \((x_i, y_i)\).

Finally, they run a GMW-like \(\mathsf{CMP}\) over \(\{\langle x_i \leq_? y_i \rangle\}_1^{\ell/k}\) and \(\{\langle x_i =_? y_i \rangle\}_1^{\ell/k}\) to get \(\langle x \leq_? y \rangle\). Now the new cost is \(O(2^{\ell/k} \cdot k)\). With a proper \(k\), the cost can be lower than the typical GC/GMW approach, as OT is generally cheaper. This protocol does not support preprocessing like GForce, but the overall communication cost is modest (\(90{\sim}120\) bits per input bit).

Below we pose a cryptographic challenge on the surface, which could be a scientific computation problem in disguise.

Challenge 1. How to implement an even more efficient \(\mathsf{CMP}\)?

Bitwidth and Overflow Issues, Truncation and Wrap-Around

Dot products over fixed-points would easily overflow, i.e., the absolute value exceeds \(p/2\) for a \(p\)-sized plaintext space.

As the most significant (\({\sim}8\)) bits matter more empirically, na"ive truncation is done by MiniONN, SecureML, and some subsequent (\(3\)PC) frameworks using SS (e.g., (Juvekar, Vaikuntanathan, and Chandrakasan 2018; Mishra et al. 2020)). To truncate \(m\) bits, the server and the client locally divide their respective arithmetic SS \(\langle x \rangle_S = x - r \bmod p\) and \(\langle x \rangle_C = r \bmod p\) by \(2^m\).

However, an error occurs when a wrap-around happens in the secret share, i.e., \(x < r\), so \(\langle x \rangle_0 = x - r + p\). In this case, \(\langle x \rangle_0 / 2^m + \langle x \rangle_1 /2^m = (x + p)/2^m \neq x/2^m\). The error probability is proportional to the message’s magnitude and \(p\). \(p\) needs to be large to suppress the error probability. The increased bitwidth (i.e., \(\lceil \log_2 p \rceil\)) leads to a higher communication cost and bulky circuits in GC/GMW for non-linear layers.

Truncation protocol of GForce (Ng and Chow 2021) outputs \(\langle x/2^m \rangle = \langle x \rangle/2^m + \langle b \rangle \cdot \lfloor p/2^m \rceil\), which offsets the wrap-around error by a wrap-around detection sub-protocol that outputs \(\langle b \rangle = 1\) if \(x < r\); \(0\) otherwise. There still could be an off-by-one error, but the impact on inference accuracy is negligible (Ng and Chow 2021; Dalskov, Escudero, and Keller 2020).

GForce proposes an efficient sub-protocol that computes \(\langle b \rangle\) with a constant multiplication (\(W\)) over additive SS (\(\langle X \rangle\)). It leverages the fact that wrap-around happens when the following conditions are both met: \(\langle x \rangle_0 > p/2\) and \(\langle x \rangle_1 < p/2\), assuming that \(x < p/2\) (Veugen 2012). This assumption can be met by swapping the \(\mathsf{ReLU}\) layer before the truncation or offsetting \(x\) by a large public constant \(L\) first and then subtracting the truncated value by \(L/2^m\).

The server generates a random SS \(\langle x \rangle_1 = r\) offline and eventually derives \(\langle b \rangle = W\langle X \rangle\) where \(W = (\langle x \rangle_1 <_? p/2)\) and \(\langle X \rangle = \langle \langle x \rangle_0 >_? p/2 \rangle\) using the AHE-to-SOS trick. Since the client knows \(\langle x \rangle_0\), it can locally compute \(X\) and send \(\langle X \rangle_1\) to the server with an additive mask.

Most MPC-based frameworks for MPC frameworks also face the fixed-point issues and need truncation after dot products. As they propose their own special kind of SS, they also come with their truncation protocols.

Quantized Neural Network (QNN)

Inputs, (intermediate) outputs, and weights of a QNN (Hubara et al. 2017) are all fixed-points. QNN can be trained from scratch or post-training quantization (quantizing a trained DNN in floats), possibly fine-tuned using training data.

QNNs are promising alternatives for crypto-processing as they tolerate limited-precision (\({\sim}8\)-bit) computation.

We highlight two works at two ends of the spectrum in a sense. “QuantizedNN” (Dalskov, Escudero, and Keller 2020) directly adopted a quantized inference scheme (Jacob et al. 2018) (originally designed for reducing the model size) to simplify the arithmetics and activations.

GForce (Ng and Chow 2021) adopts SWALP (stochastic weight averaging in low-precision training) (G. Yang et al. 2019) that trains a quantized model for inference with \({<}1\) percentage point (pp) of accuracy drop, further abstracts the (de)quantization to “SRT layers,” with a more efficient truncation protocol, and analytically proves that the output distribution is close to such stochastic rounding after truncation. Interestingly, SRT is also GPU-friendly using the AHE-to-SOS trick.

With what the two previous subsections discussed, we ask:

Challenge 2. How to utilize GPU for better performance, possibly with tricks to deal with the low-bitwidth constraint?

Challenge 3. Is there any other secure protocol for non-linear functions that can be made to fit with the AHE-to-SOS trick?

Improving Efficiency of HE Operations

SOS computation reduces only online latency. Many mixed frameworks use various HE tricks to reduce the overall latency.

Denoising. Gazelle uses tight HE parameters to reduce latency, imposing a tight noise quota over HE operations (also see the Section on HE Optimization). After each linear layer, it “refreshes” \([y + r]\), where \(y\) is the intermediate result, and \(r\) is a mask from additive SS, by sending it to the client to decrypt and re-encrypt it to clear the noise (vs. running the entire NN without the client). This requires a good network condition, and the client must remain online.

A tempting trick is to let the client receive \(y\), possibly with “noise” (but not masks) injected for efficient non-linear computation.

Such heuristics were quickly proven insecure as a malicious client can average out the noise with multiple queries (Wong et al. 2020).

Optimizing/Reducing Rotations. SIMD is widely adopted, e.g. (Liu et al. 2017), but its rotation is not cheap (the Section on HE background knowledge).

Gazelle handles linear layers by dedicating all SIMD slots in an HE ciphertext to a single inference query to reduce its latency.

To align the slots for summation, it proposes a slot encoding and rotation scheme to reduce the number of ciphertexts the server sends back.

LoLa (Brutzkus, Gilad-Bachrach, and Elisha 2019) (a pure-LHE framework) also uses SIMD in the same way while minimizing the rotation cost according to the overall NN architecture.

GALA (Q. Zhang, Xin, and Wu 2021) further reduces the use of rotations. First, some can be cheaply replaced by rotating the plaintext weights during encoding.

Second, the server can skip some rotation-and-sum on the ciphertexts by sending intermediate encrypted results with an additive mask to the clients, who will then decrypt them and (cheaply) sum the additively masked values during denoising.

“FalconI” (Li et al. 2020) applies Fast Fourier Transform (FFT) on both weight tensors and input ciphertexts. Convolution then becomes point-wise multiplication. This approach avoids rotations. However, it is only suitable for (interactive) S/C frameworks and not pure-HE frameworks because it requires the client to perform inverse FFT on the resulting SS (converted from HE ciphertexts) for the subsequent non-linear layers.

Interestingly, this CVPR paper (Li et al. 2020) did not emphasize that it is motivated by avoiding rotation. This inspires the challenge and open problem below, which probably needs insights into the NN computations.

Challenge 4. How to reduce the costs of HE SIMD/rotations?

Open Problem 4. We see various improvements in the mixed approach. Are there other scientific computation/machine learning techniques with cryptographic implications to explore?

MPC-based Inference/Training Frameworks

Many frameworks employ multiple non-colluding servers to run MPC. SS operations for MPC are very efficient. In general, they have the best performance. Many support private training.

Major Developments for MPC-based Inference

To support outsourced inference, SecureML (Mohassel and Zhang 2017) distributes the arithmetic shares of the weights to \(2\) servers to evaluate the matrix multiplication or convolution via Beaver’s trick. It evaluates non-linear layers via GC or piecewise linear approximation (see the Section on non-linear layers). It also supports training over SS.

ABY2.0 (Patra et al. 2021) supports more (online-)communication-efficient and higher fan-in multiplication and \(\mathsf{CMP}\) by using a new kind of additive SS.

Say No to Beaver. Quotient (Agrawal et al. 2019) uses OT and GC to avoid (the expensive offline phase for) Beaver triplets, which improves the overall throughput. It is specifically designed for ternarized NNs with weights confined to \(\{-1, 0, 1\}\). However, Quotient’s efficiency and accuracy are only demonstrated on small NNs with a few linear layers (using matrix multiplication).

More Non-colluding Servers.

Having more servers allows more options, e.g., a third server can aid in preparing triplets without interactions between two servers. But it increases the risk. They might use \(4\) servers (see Table 2), but an adversary still only needs \(2\) servers for a total break (Rachuri and Suresh 2020; Byali et al. 2020; Dalskov, Escudero, and Keller 2021).

Table 2: Frameworks Under Non-colluding Assumptions or with Malicious Security

Framework	Number of Servers	Guarantee
SecureML (Mohassel and Zhang 2017)	\(2\)	\(-\)
Quotient (Agrawal et al. 2019)	\(2\)	\(-\)
ABY2.0 (Patra et al. 2021)	\(2\)	\(-\)
Piranha (Watson, Wagh, and Popa 2022)	\(\geq 2\)	\(-\)
CrypTen (Knott et al. 2021)	\(\geq 2\)	\(-\)
QuantizedNN (Dalskov, Escudero, and Keller 2020)	\(2/3\)	Abort
Chameleon (Riazi et al. 2018)	\(3\)	\(-\)
CrypTFlow (Kumar et al. 2020)	\(3\)	\(-\)
CryptGPU (Tan et al. 2021)	\(3\)	\(-\)
SecureNN (Wagh, Gupta, and Chandran 2019)	\(3\)	Abort
ABY3 (Mohassel and Rindal 2018)	\(3\)	Abort
FalconN (Wagh et al. 2021)	\(3\)	Abort
AdanInPrivate (Attrapadung et al. 2022)	\(3\)	Abort
Blaze (Patra and Suresh 2020)	\(3\)	Fair
Swift (Koti et al. 2021)	\(3/4\)	G.O.D.
Fantastic 4 (Dalskov, Escudero, and Keller 2021)	\(3/4\)	G.O.D.
Flash (Byali et al. 2020)	\(4\)	G.O.D.
Trident (Rachuri and Suresh 2020)	\(4\)	Fair
GarbledNN (Ball et al. 2019)	\(-\)	Abort
XONN (Riazi et al. 2019)	\(-\)	Abort
Muse (Lehmkuhl et al. 2021)	\(-\)	Client

Chameleon (Riazi et al. 2018) is a mixed framework that speeds up ABY with various tricks. It computes some gates over boolean SS (by GMW) and more advanced protocols by exploiting \(3\) servers, e.g., a communication-cost-saving variant of Du–Atallah protocol (W. Du and Atallah 2001) for efficient multiplication over additive SS. ABY3 (Mohassel and Rindal 2018) extends ABY to \(3\)PC over \(3\) servers. It proposes a new kind of \(2\)-out-of-\(3\) additive shares for less communication cost, which is generated via a pseudorandom function by exchanging short secret seeds. No Beaver’s triplets are used.

SecureNN (Wagh, Gupta, and Chandran 2019) and “FalconN” (Wagh et al. 2021) propose \(3\)PC variants of DGK comparison protocol using additive SS to outperform (non-colluding 3PC) GC/GMW-based ABY3 (Mohassel and Rindal 2018).

Trident (Rachuri and Suresh 2020) introduces the \(4\)-th non-colluding server, which allows more SS kinds, enabling more efficient secure multiplication and comparison, and moving much computation and communication offline. With \(32\)-CPU-core parallelism, Trident exhibits a much higher online throughput than ABY3, SecureNN, and FalconN in evaluation by orders of magnitude. In principle, many protocols can also be implemented in parallel.

Flash (Byali et al. 2020), Blaze (Patra and Suresh 2020), and Swift (Koti et al. 2021) also employ \(4\) non-colluding servers to enhance the throughput. They aim to defend against malicious adversaries, to be discussed in the Section on malicious security.

Fluctuating Weights in Limited-bitwidth Training

Private and outsourced training frameworks run backward propagation with millions of iterations beyond forward propagation in inference. The only purely-crypto frameworks demonstrating reasonable training time (hours/days for common NNs) use SS under non-colluding assumptions (Tan et al. 2021; Wagh et al. 2021; Attrapadung et al. 2022).

Fluctuating weights make private training suffers even worse from fixed-point issues since increasing magnitudes (of weights, gradients, and intermediate inputs) in a low-bitwidth environment makes overflow happens easier. Meanwhile, the weights may become zeros when their magnitudes decrease, nullifying the training as the scaling factor may be too small. Most frameworks are yet to demonstrate running large NNs, e.g., VGG, and more complicated datasets, e.g., CIFAR-10/100.

Approaches for inference discussed in the Section on mixed bitwidth do not apply: With a higher overflow chance, fixed-scale truncation damages the training easily. Yet, we note that some underlying principles might remain relevant –

One may aim for quantized NN (QNN) using low-bitwidth training. BatchNorm “for” non-linear function in the Section on non-linear layers might also “helps.”

High Bitwidth

The private training frameworks usually use the \(64\)-bit ring (\(\mathbb{Z}_{2^{64}}\)) for their underlying SS. In contrast to the \(32\)-bit (or less) ring used by S/C frameworks (for oblivious inference), SS in \(\mathbb{Z}_{2^{64}}\) doubles the communication and computation costs as it halves the throughput of vectorized operations on CPU/GPU, e.g., Intel AVX. High bitwidth also leads to bulk circuits for the non-linear layers, harming the performance.

BatchNorm

Batchnorm layers in private training are supported by FalconN (Wagh et al. 2021) using \(3\) servers. Both the inputs in the forward propagation and the gradients in the backward propagation are normalized in a smaller range to cater to the low-bitwidth environment. Unlike inference, BatchNorm in training requires division and inverse square root where the divisors should be private and unknown prior to training, while it is public and fixed in inference. FalconN thus resorts to a costly iterative method (see the Section on non-linear layers) while leaking the input magnitude.

Adam

“AdamInPrivate” (Attrapadung et al. 2022) adopts adaptive moment estimation (Adam), a more advanced SGD algorithm for training. To stabilize the gradient fluctuation between training batches, it scales the gradient by \(1/\sqrt{G}\), where \(G\) is the moment, i.e., the sum of the squares of the previous gradients. AdamInPrivate computes \(1/\sqrt{G}\) using the techniques in the Section on non-linear layers.

Low-bitwidth QNN Training with “Small” Fixed-point Gradients

BatchNorm and Adam cannot fully resolve the bitwidth hurdles. When a DNN attains a certain level of accuracy, \(\Delta w\) (for updating the weight to \(w - \alpha \cdot \Delta w\)) may become so small that it has to be accumulated for many iterations before making noticeable changes to the weights. The training ceases to progress because these small gradients are discarded.

Quotient (Agrawal et al. 2019) adopts a QNN training scheme WAGE (S. Wu et al. 2018) (constraining weights, activations, gradients, and errors) to update the weights stochastically according to the magnitude of the gradient, such that small gradients still have an impact on the big weight. Yet, its attained accuracy is still inferior to

floating-point training (S. Wu et al. 2018). We note that perhaps deterred by the expensive GC for stochastical updates, other private training frameworks are yet to integrate low-bitwidth training schemes.

Softmax

Unlike inference, where the output layer usually outputs the index of the maximal element of its inputs, training requires the output layer to map its input via a differentiable function to enable backward propagation. A common choice is \(\mathsf{softmax}(\mathbf{x}) = (e^{x_i}/\sum_j e^{x_j})_{i}\). Most schemes compute it with piecewise linear approximation.

CrypTen (Knott et al. 2021) proposes a more efficient and accurate approach combining private division and the limit characterization of \(e^x\) (the Section on non-linear layers).

6. GPU for Training

Consider the dot product \(\sum_i \langle w_i \rangle \cdot \langle x_i \rangle\), the bitwidth of the SSs cannot exceed \(26\) bits, not to mention redundant bitwidth to cater for additions.

CryptGPU (Tan et al. 2021) utilizes GPUs for private training. It picks the \(64\)-bit ring (\(\mathbb{Z}_{2^{64}}\)) for SS, which exceeds the bitwidth limit of GPUs. It thus decomposes an SS \(\langle X \rangle\) into \(2^{48} \langle X_4 \rangle + 2^{32} \langle X_3 \rangle + 2^{16} \langle X_2 \rangle + \langle X_1 \rangle\). Multiplying the low-bitwidth sub-SSs \(\{\langle X_i \rangle\}_1^4\) requires many cross-term multiplications, offsetting some performance gain from GPU.

Short Summary

The high bitwidth training requirement conflicts with the low-bitwidth crypto environment. (Batchnorm) normalizes the operands into a smaller range. Still, the gradients may become too small and easily underflow as the training goes on. The loss function \(\mathsf{softmax}\) also requires accurate approximation. With the current techniques, we still need relatively high bitwidth representation, harming the training throughput, and the resulting accuracy could be shy of \({>}30\)pp: CryptGPU (Tan et al. 2021) only attains \({\sim}60\%\) accuracy in CIFAR-10, while GForce (Ng and Chow 2021) gets to \({>}90\%\) in oblivious inference (Ng and Chow 2021). Private training still desires more ML research, tackling the following two challenges.

Challenge 5. How to cater dynamic weights in secure training?

Challenge 6. How to privately, efficiently, and accurately evaluate (both linear and non-linear) layers in low-bitwidth?

Non-Linear Layers for Training and RNNs

In training, BatchNorm needs private division \(1/y\), inverse square root \(1/\sqrt{y}\); and \(\mathsf{softmax}\) needs exponential function \(e^x\).

SiRnn (Rathee et al. 2021), as an oblivious-inference-only framework, also proposes protocols for these functions to support recurrent NN (RNN) (Hochreiter and Schmidhuber 1997), e.g., with gated recurrent unit (K. Cho et al. 2014) or LSTM cells, which is good at sequential data like voice records and articles. RNN requires \(e^x\) for \(\mathsf{sigmoid}\), \(\mathsf{tanh}\), and normalization, but their piecewise linear approximation (Liu et al. 2017; Mohassel and Zhang 2017) unbearably fails.

Piecewise Approximation partitions non-comparison-based functions, e.g., \(\mathsf{sigmoid}\), into many linear functions, and uses \(\mathsf{CMP}\) via GC to locate the piece of the input. SecureML and MiniONN adopt it. The accuracy increases with more dissections, but more \(\mathsf{CMP}\) and multiplexers harm the performance.

Private Division is known to be more expensive as it frequently invokes the truncation protocol (cheaper as the divisor is public).

FalconN (Wagh et al. 2021) computes \(\langle 1/y \rangle\) with Goldschmidt’s method. With an initial guess \(\langle w_0 \rangle\), it computes the approximation \(\langle w_{i} \rangle = \langle w_{i-1} \rangle \cdot (1 + \langle \epsilon_{i-1} \rangle)\) with the error correction term \(\langle \epsilon_i \rangle = \langle \epsilon_{i-1} \rangle^2\). (Here, we omit the scaling up and truncation.)

Each iteration can double the precision (i.e., quadratic convergence) – the absolute error \(|w_t - 1/y|\) is less than \(|w_0 - 1/y|^{2^t}\), but it takes \(1\) more communication round for each SS multiplication. It outputs \(\langle w_t \rangle \approx \langle 1/y \rangle\) after \(t\) iterations.

A good initial guess reduces the iterations needed. FalconN adopts \(\langle w_0 \rangle = 2.9142 - 2 \cdot \langle y \rangle / 2^{\alpha}\) from the prior art in private division (Catrina and Saxena 2010). \(\alpha\) is the (unprotected) magnitude of \(y\) (\(2^\alpha\!\leq y\!\leq 2^{\alpha + 1}\)). The fixed-point representation of \(w_0\) and \(y\) are scaled up to precision \(\alpha + 1\) to avoid value underflow.

CrypTen (Knott et al. 2021) computes \(\langle w_0 \rangle = 3 \cdot \langle e^{0.5-y} \rangle + 0.003\) (see below for \(\langle e^{y} \rangle\)). CryptGPU (Tan et al. 2021) assumes \(y\) is bounded in \([1, Y]\), which is applicable to \(\mathsf{softmax}\) in private training but may not to \(\mathsf{sigmoid}\) and \(\mathsf{tanh}\) in RNN. The initial guess is set to \(w_0 = 1/Y\).

AdamInPrivate (Attrapadung et al. 2022) proposes to privately extract magnitude \(\alpha\) by a circuit, use it to shift \(y\) to \(1 - y' \in [0.5, 1)\), and compute \(\langle 1/(1 - y') \rangle = \langle 1 + y' + y'^2 + \ldots \rangle = \langle 1+y' \rangle \cdot \langle 1+y'^2 \rangle \cdot \langle 1+y'^4 \rangle \cdots\) by \(O(\log_2 t)\) squaring and multiplications for a \(t\)-degree approximation, and scale \(\langle 1/(1 - y') \rangle\) back to \(\langle 1/y \rangle\).

Inverse Square Root. \(\langle 1/\sqrt{y} \rangle\) can be evaluated by Newton’s iterative method \(w_i = \langle w_{i-1} \rangle \cdot (3 - \langle y \rangle \cdot \langle w_{i-1} \rangle^2)/2\) with quadratic convergence. AdamInPrivate privately extracts in a circuit \(\lfloor \alpha/2 \rceil\) and hides \(w_0\)’s value. FalconN picks \(w_0 = 2^{\lfloor \alpha/2 \rceil}\).

Exponential Function. For \(\langle e^x \rangle\), CrypTen (Knott et al. 2021) approximates \(\langle e^x \rangle\) more efficiently by computing the limit characterization \((1 + \langle x \rangle/2^t)^{2^t}\). It takes \(t\) iterations of SS multiplications to reduce relative error to \(e^{O(-x^2/2^t)}\) for \(|x| < 2^t\).

Lookup Table. Borrowing memory-saving tricks in embedded systems, SiRnn (Rathee et al. 2021) extends a provably precise lookup approach for getting a good initial guess before using iteration to improve upon the approximation. Namely, it obliviously looks up \(d\)-digit \(\langle \mathsf{exp}({2^{d\cdot (i-1)} x_i} \rangle)\) over \(\langle x_i \rangle\) for \(x = x_k || \cdots || x_1\) and multiplies the shares as \(e^x = \mathsf{exp}({2^{d\cdot (k-1)} \cdot x_k + \cdots + 2^d \cdot x + x_1})\). An upside is that the oblivious lookup can be parallelized, while iterative approaches are inherently sequential.

The above approaches only work on additive shares. Glyph (Lou et al. 2020) uses the lookup table implemented by TFHE and BGV-HE to compute \(\mathsf{sigmoid}\) and \(\mathsf{softmax}\). Yet, it is impractically slow due to the overhead caused by the FHE schemes. Lately, Heath and Kolesnikov (Heath and Kolesnikov 2021) propose one-hot garbling that allows efficient privacy-free lookup tables in garbled circuits. It would be interesting to know if it can speed up non-linear layers, especially in a high-latency communication environment where GC trumps OT.

To sum up, many tricks are inspired by numerical approximations, possibly with a new angle, such as the lookup approach for iterative computations. Their accurate approximations are also crucial for private training. We pose two challenges:

Challenge 7. How to efficiently and accurately approximate \(x/y\), \(1/\sqrt{y}\), \(e^x\), \(\mathsf{sigmoid}(x)\), and \(\mathsf{tanh}(x)\) for secret \(x\) and \(y\)? More broadly, is there any other crypto-friendly numerical method for mathematical functions useful for NN?

Challenge 8. Can we generalize the lookup approach or extend other low-bitwidth tricks of embedding systems to other non-linear functions for more efficient approximations?

Practical Deployment Issues

Neural Network Architecture Optimization

Tuning NN architecture can cut the cost of cryptographic NN computation with moderate inference accuracy degradation.

Pruning outsourced inference would let the server learn the number of zeroed weights from how much computation is saved. Such leakage is not a concern in non-outsourced inference. Still, a custom implementation of SS operations is needed to take advantage of zeroed weights as they are hidden by SS, abandoning off-the-shelf optimized math libraries. This asks for dedicated customization and secure programming effort to ensure no potential side-channel leakage.

Open Problem 5. How to build a leakage-free data-oblivious library exploiting data-dependent optimization like pruning?

Cost Optimizers tune the architecture to optimize an objective function, factoring in the inference accuracy and the cost of cryptographic primitives. NASS (Bian et al. 2020) performs an automatic search for NN architecture and HE parameters to attain the best performance and accuracy over Gazelle (Juvekar, Vaikuntanathan, and Chandrakasan 2018). COINN (Hussain et al. 2021) optimizes over the bit-width of operands in each linear layer.

Weight Clustering. Observing \(\sum{w_i \cdot x_i}\) over \(N\) weights \(\{w_i\}\) can be factorized into \(\sum_{i \in [1, V]}{w_i \sum_{j \in S_i}{x_j}}\) over \(V\) unique weights after clustering, where \(S_i\) is the index set, COINN uses \(N\) OTs to select and accumulate \(\sum_{j \in S_i}{X_j}\) for \(i \in [V]\), resulting in \({\approx} VN\ell\) bits of communication over \(\ell\)-bit arithmetic shares (vs. \({\approx}N\ell^2\), as in the Section on offline-online computation).

Then, it computes the shortened dot product over size-\(V\) vectors with \(V\ell^2\) bits of communication. The total cost is reduced to \(V\ell(N + \ell)\) with COINN’s bit-width optimization (\(N \gg \ell\)) when \(V < \ell\).

Reducing \(\mathsf{ReLU}\). With the huge performance gap between polynomial approximation and \(\mathsf{CMP}\), Delphi’s planner (Mishra et al. 2020) searches for NNs that replace \(\mathsf{ReLU}\) layers by quadratic approximation with mild accuracy degradation. SafeNet (Lou et al. 2021) provides a better tradeoff by a more fine-grained replacement of \(\mathsf{ReLU}\) by approximation on some channels instead of a whole layer.

CryptoNAS (Ghodsi et al. 2020) reduces the number of \(\mathsf{ReLU}\)’s by observing that a \(\mathsf{ReLU}\) layer in ResNet may skip some or even all inputs, and just outputs identical values. DeepReDuce (Jha et al. 2021) further subsamples the inputs to \(\mathsf{ReLU}\) layers. It adopts knowledge distillation (J. H. Cho and Hariharan 2019) to compensate for the accuracy loss, which retrains the \(\mathsf{ReLU}\)-reduced NN with the input-output pairs of the original NN. Surprisingly, the retrained NN may even attain higher accuracy than the original NN.

Despite their empirical performance, they do not appear to be the optimal search for \(\mathsf{ReLU}\) reduction. We thus ask:

Challenge 9. How to “optimally” approximate \(\mathsf{ReLU}\) layers while mildly affecting (or even improving) accuracy?

Cost optimization can be seen as a pursuit complementary to the open problem for cyrpto-friendly machine learning techniques, which explores the use of polynomials as crypto-friendly operations to approximate non-linear layers.

ML research for broader classes of crypto-friendly computations (beyond polynomials) remains largely unexplored. Despite this, this SoK discussed two different kinds of fusing from the system (nGraph-HE (Boemer, Lao, et al. 2019)) and crypto (GForce (Ng and Chow 2021)) communities. The latter can minimize non-crypto-friendly computations.

Broadly:

Open Problem 6. Are there other “fusing” opportunities that can reduce cryptographic operations in PPNN?

Hyperparameters affect how ML algorithms perform. Hyperparameter tuning aims to find out the best configuration of the training algorithm that will output a model generalizing to new data well. There is growing attention to hyperparameter optimization (HO) since tuning procedures could be tedious.

Open Problem 7. Are there any HO opportunities beneficial to PPNN, say, minimizing the cost of cryptographic NN computation while maintaining an “acceptable” accuracy level?

Open Problem 8. Can we realize “private training with HO”?

Deploying Optimized HE Frameworks

To sustain the magnitude growth in iterated ciphertext operations, pure-LHE frameworks using BFV-HE or BGV-HE, e.g., CryptoNets and FasterCryptoNets (Chou et al. 2018) deal with the overflow issue by picking large plaintext space. CKKS-HE

allows discarding the least significant bits by rescaling; each such operation requires large HE parameters. These enlarged HE parameters increase the runtime and communication cost. It explains why pure-LHE frameworks are not efficient enough for deep NNs.

HE parameters include the finite-field size for the plaintext (i.e., bitwidth), the degree of the polynomial representing the ciphertexts (often also the numbers of SIMD slots), and the coefficient’s moduli of the polynomial (determining the number of “levels” of HE operations and noise tolerance). Each operation accumulates noise in a ciphertext, which may eventually destroy its plaintext. HE parameters determine how much noise it can withstand.

It is not easy for non-cryptographers to pick the optimal parameters under constraints with cryptographic implications. Large parameters lead to larger ciphertexts and more expensive computations. For a good balance of security and efficiency, one should carefully choose tight parameters if possible.

Challenge 10. How to guide non-cryptographers to select “tight” HE parameters or avoid the troubles of the noise?

Compilers are proposed to do it w.r.t. NN architecture. We defer them to the Section on compilers for their multiple purposes (Boemer, Lao, et al. 2019).

Selecting tight HE parameters is critical for performance. A few frameworks automatically pick just-enough choices to prevent overflow with operational costs confined. They also select scaling factors for the fixed-point representation.

CHET (Dathathri et al. 2019) derives HE parameters based on the training dataset and the computation graph (for the NN architecture). SEALion (Elsloo, Patrini, and Ivey-Law 2019) adopts a similar approach. nGraph-HE2 (Boemer, Costache, et al. 2019) selects small parameters (\(32\)-bit moduli) to reduce CPU instructions for HE.

Optimizing the data layout can lower rotation costs (e.g., for dot product, see the Section on efficient HE). Most frameworks automatically encode (plaintext/encrypted) tensors into the HE polynomials, without developers noticing the underlying data layout.

CHET (Dathathri et al. 2019) further optimizes the data layout to minimize the overall rotation cost, as different rotations cost differently.

Fusing or skipping operations is common in compiler optimization. nGraph-HE (Boemer, Lao, et al. 2019) parallelizes HE operations (on CPU), exploiting the SIMD of HE over the batches of inputs, fusing the multiplications in BatchNorm layers, and skipping some HE operations when the plaintext is \(0, 1\), or \(-1\). nGraph-HE2 (Boemer, Costache, et al. 2019) groups up or skips expensive denoising.

Optimizing over the hardware intrinsics is done by PlaidML-HE (Chen et al. 2019) for more efficient HE operations and linear layers. It covers CPUs and GPUs of various brands and CKKS-HE (Cheon et al. 2017) for its residue number system.

If we had an HE scheme that could be instantiated with small parameters, it immediately reduces the communication cost. Likewise, cutting the bootstrapping time (e.g., of TFHE) also reduces the latency. Cryptographers’ research efforts are mostly needed for the problems/challenges below.

Open Problem 9. How to improve HE’s performance?

Challenge 11. How to perform low-latency inference under limited-bandwidth conditions without non-colluding servers?

Challenge 12. How to efficiently realize secure outsourcing of inference for deep NNs without non-colluding assumptions?

Compilers for Rapid Development and Optimization

Developer-Friendly Compilers. Many works proposed a specific compiler that compiles a (plaintext) NN, including the architecture and the weights, into a PPNN, often with optimized cryptographic computation. This allows coding with a standard machine-learning library or high-level APIs without knowing much about (optimizing) cryptographic computation, reducing laborious hand-engineering and possible coding errors.

Graph-Based Compilers transform an NN representation of an NN library, e.g., TensorFlow or PyTorch, into the “cryptographic version” for oblivious inference. They include nGraph-HE/2 (Boemer, Lao, et al. 2019; Boemer, Costache, et al. 2019), PlaidML-HE (Chen et al. 2019), and CrypTFlow (Kumar et al. 2020).

Custom APIs are proposed by some frameworks to help developers adopt them. EzPC (Chandran et al. 2019) is a general compiler for \(2\)PC that converts its Python-like source code to C++, calling ABY API functions for oblivious inference with 2 non-colluding servers. XONN (Riazi et al. 2019) supports high-level API for BNN layer specification and translates an NN description from other DNN libraries into its API. SEALion (Elsloo, Patrini, and Ivey-Law 2019) uses Keras-like syntax for implementing PPNN, while CHET (Dathathri et al. 2019) uses TensorFlow-like syntax. CrypTen (Knott et al. 2021) proposes PyTorch-style APIs for \(2\)PC protocols (mainly from FalconN’s protocol (Wagh et al. 2021)).

GPU Platform for Arithmetic SS. Piranha (Watson, Wagh, and Popa 2022) is a platform for MPC from arithmetic SS to run on top of GPU. Its modular design allows easier integration of new SS-based protocols (for a certain layer) than re-implementing the entire framework. These compilers bring convenience to developers.

However, PPNN researchers often still need much engineering effort to implement specific tricks they devised, let alone re-implement existing ones for comparison when they are often implemented with different languages on top of different libraries with slightly different low-level optimization. To let researchers focus on what they are good at and save resources from
incessant replications of old results (e.g., \(96\) cores (Badawi et al. 2021), Nvidia V100 GPU (Ng and Chow 2021; Tan et al. 2021; Badawi et al. 2021; Watson, Wagh, and Popa 2022), processing \(1\)TB of data for an encrypted query (Chou et al. 2018)), a rapid benchmarking platform is desired:

Challenge 13. Can we build a universal compiler that enables rapid prototyping and allow uniform experimental comparison?

e.g., CrypTen, Delphi, EzPC, GForce

Optimization. EzPC (Chandran et al. 2019) optimizes performance over the choices of A/B/Y SS for oblivious (program evaluation and) inference. Most others optimize arithmetic HE:

Challenge 14. Can we build an end-to-end compiler like PlaidML-HE over other major HE schemes such as TFHE?

Leakages of Metadata and Difficult-to-Hide Information

Convolution Parameters. Most frameworks leak the stride, padding, and kernel size in convolution layers. When using circuit-based primitives in the outsourced setting (e.g., TFHE, GC, and GMW), adversaries can derive them from the circuit’s topology. Likewise, they can be leaked from the computation steps by an outsourced server unless they are locally done.

Dimensions of Layers refer to the input and output size of the layers. For outsourced or server/client frameworks, they can be derived from the intermediate SSs or HE ciphertexts. For pure-HE inference frameworks, the client does not see the intermediate ciphertexts and hence does not see the leakage.

Types of Layers are similar to dimensions since PPNN frameworks do not hide the computed functions in general.

Total Number of Layers. Leaking the dimension also leaks the total number of layers. LHE frameworks still leak this information because the client can deduce the number of multiplications performed. Usually, a linear or activation layer requires one.

Are Practitioners Willing to Compromise?

The state-of-the-art private training using \(3\) GPUs is still far from the performance of plaintext training. Meanwhile, the ML community has started considering solutions using trusted execution environments and lightweight cryptographic outsourcing protocols for leveraging (untrusted) GPUs (Ng et al. 2021). With the performance gap from plaintext training, some might care less about trust assumptions or malicious security.

Open Problem 10. Is there any gap between theoretical security guarantees and what practitioners are (un)willing to trust? How should those perspectives inform PPNN research efforts?

The answer depends on the application scenarios and deployment settings. On one hand, there are highly sensitive scenarios, e.g., child exploitation imagery detection, in which one might expect the highest security level.

On the other, it can be a life-saving effort to speed up the progress in, e.g., cancer diagnosis (Ng et al. 2021), genomic precision medicine, drug-target interactions (Hie, Cho, and Berger 2018), and reliance on the non-colluding assumption could become a secondary concern (Chow, Lee, and Subramanian 2009).

One may have faith in a privacy-respecting government or privacy advocates for the needed trust. Meanwhile, industry players might not welcome non-colluding assumptions since the idea of trusting competitors can be illusory to some.

Status Quo in Accuracy/Latency/Throughput

We integrate evaluation results presented by the papers covered by this SoK in the same plots for general trends.

Each framework shines in its way in its targeted settings. We highlight noteworthy points in the space. We then present re-evaluations of the most promising frameworks we identified.

Below, we discuss typical benchmark datasets in the literature. More complicated tasks often require a more complex NN architecture with more internal parameters for high accuracy.

MNIST is a dataset for classifying black-and-white hand-written digitals over \(28\times 28\) images, which can be handled via a multilayer perceptron (MLP) NN with \(1\) fully-connected layer at \({>}99\%\) accuracy. It can no longer demonstrate the superiority of new advancements in rapidly developing PPNN research.

CIFAR-10/100 became popular for benchmarking. They are datasets consisting of 10/100 classes of \(32 \times 32\) colorful images of vehicles and animals, e.g., dog, ship, and truck, which are harder to classify than the simpler MNIST, and require convolution layers for better accuracy. VGG-16 (Simonyan and Zisserman 2015), having \(16\) linear layers, is a commonly chosen architecture to handle CIFAR-10/100. ResNet (He et al. 2016) can attain a higher accuracy but also incurs longer inference latency as it has more linear layers.

ImageNet is an even more challenging object recognition dataset. It consists of \({>}14\) millions \(224 \times 224\) colorful images with \({>}20000\) classes. Handling this dataset requires capacity beyond current PPNN frameworks.

Still, one (Rathee et al. 2020) may process \(224 \times 224\) (ImageNet-scale) images to estimate its performance on such large images and claims that it loses no accuracy given enough bitwidth.

A few frameworks (Chou et al. 2018; Wagh et al. 2021) shrink the dataset into Tiny ImageNet with \(120,000\) \(64 \times 64\) images under \(200\) classes to demonstrate their ability beyond CIFAR-10/100. Unfortunately, they rarely provide accuracy, probably because fixed-point issues are yet to be overcome for the large NNs needed. It is hard to have a fair comparison.

To put accuracy and latency into perspective, we may also factor in:

• the problem setting (oblivious/outsourced inference or outsourced/private training),
• the chosen dataset,
• the network condition (e.g., LAN or WAN),
• the number of non-colluding servers, and
• online versus total performance.

Oblivious Inference

We summarize the performance of \(23\) frameworks marked with CIFAR-10 in our Summary of all Frameworks (except AdamInPrivate with only training benchmarks). The tests used CIFAR-10 and LAN.

• \(7\) pure-HE frameworks: CHET (Dathathri et al. 2019), HCNN (Badawi et al. 2021), FasterCryptoNets (Chou et al. 2018) (or Faster-Crypt in Tables/Figures), CryptoDL (Hesamifard et al. 2018), nGraph-HE (Boemer, Lao, et al. 2019), LoLa (Brutzkus, Gilad-Bachrach, and Elisha 2019), and SHE (Lou and Jiang 2019);

• \(13\) server/client (S/C) frameworks: CrypTFlow2 (Rathee et al. 2020), XONN (Riazi et al. 2019), Delphi (Mishra et al. 2020), GForce (Ng and Chow 2021), FalconI (Li et al. 2020), DeepSecure (Rouhani, Riazi, and Koushanfar 2018), EzPC (Chandran et al. 2019), Gazelle (Juvekar, Vaikuntanathan, and Chandrakasan 2018), MiniONN (Liu et al. 2017), GarbledNN (Ball et al. 2019), COINN (Hussain et al. 2021), SafeNet (Lou et al. 2021), and CryptoNAS (Ghodsi et al. 2020);

• \(3\) non-colluding frameworks: FalconN! (Wagh et al. 2021), CryptGPU (Tan et al. 2021), Piranha (Watson, Wagh, and Popa 2022)’s GPU-instantiation of FalconN and Fantastic 4.

We first provide an integrated report of their accuracy, latency, and throughput. Our figures aim to give readers a sense of differences among different paradigms (marked with different colors) and the significance of GPU-friendly protocols. We also aim to identify the state of the art in each paradigm. Thus, the figures only name the Pareto fronts of each paradigm, which also avoids overcrowded name tags.

Multiple data points in each figure can be contributed by a single framework over different NN architectures (all tested with CIFAR-10).

Most existing tests are on LAN, which may not be realistic. To better understand the identified state of the art, we re-evaluate them on WAN with various bandwidths to unveil which framework performs the best under a non-ideal network. It gives us clues on deployment requirements, particularly the minimal bandwidth needed for their peak performance.

For readability, we omitted \(8\) outliers, from the following \(3\) frameworks, due to their low accuracy: nGraph-HE (\(62\%\)), COINN (\(68.1\%\) – but it has another data point on the Pareto frontier for throughput), and Piranha (\(40\%\) and \(55\%\) – two data points nevertheless on the Pareto frontier for \(3.25\times 10^6\) Images/hr throughput and \(131\)ms latency).

1. Online Latency.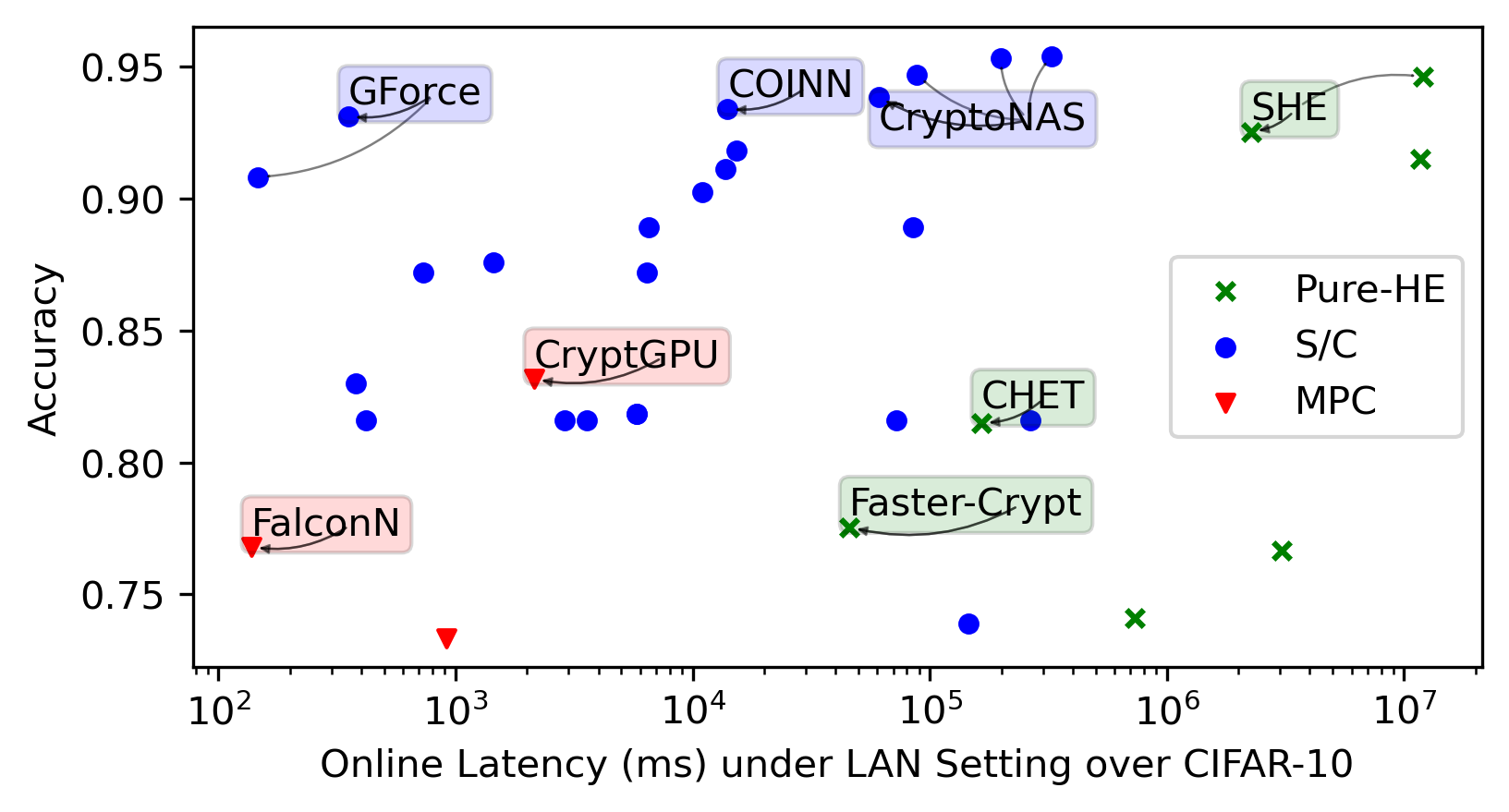

Figure 1: Online Latency of Inference on CIFAR-10 (top-left ones are better)

Figure 1 shows the inference accuracy with respect to the online latency, which is more crucial than total latency for user experiences.

GForce (Ng and Chow 2021) strikes the best balance and surprisingly outperforms non-colluding MPC frameworks like CryptGPU (Tan et al. 2021) and FalconN (Wagh et al. 2021) for inference (albeit supporting training). It may be attributed to its adoption of QNN and GPU-friendly comparison protocol. Pure-HE frameworks perform the worst in this setting.

For CIFAR-10, deep NNs are usually needed for reasonable accuracy, leading to huge HE parameters and worse performance.

2. Online Throughput.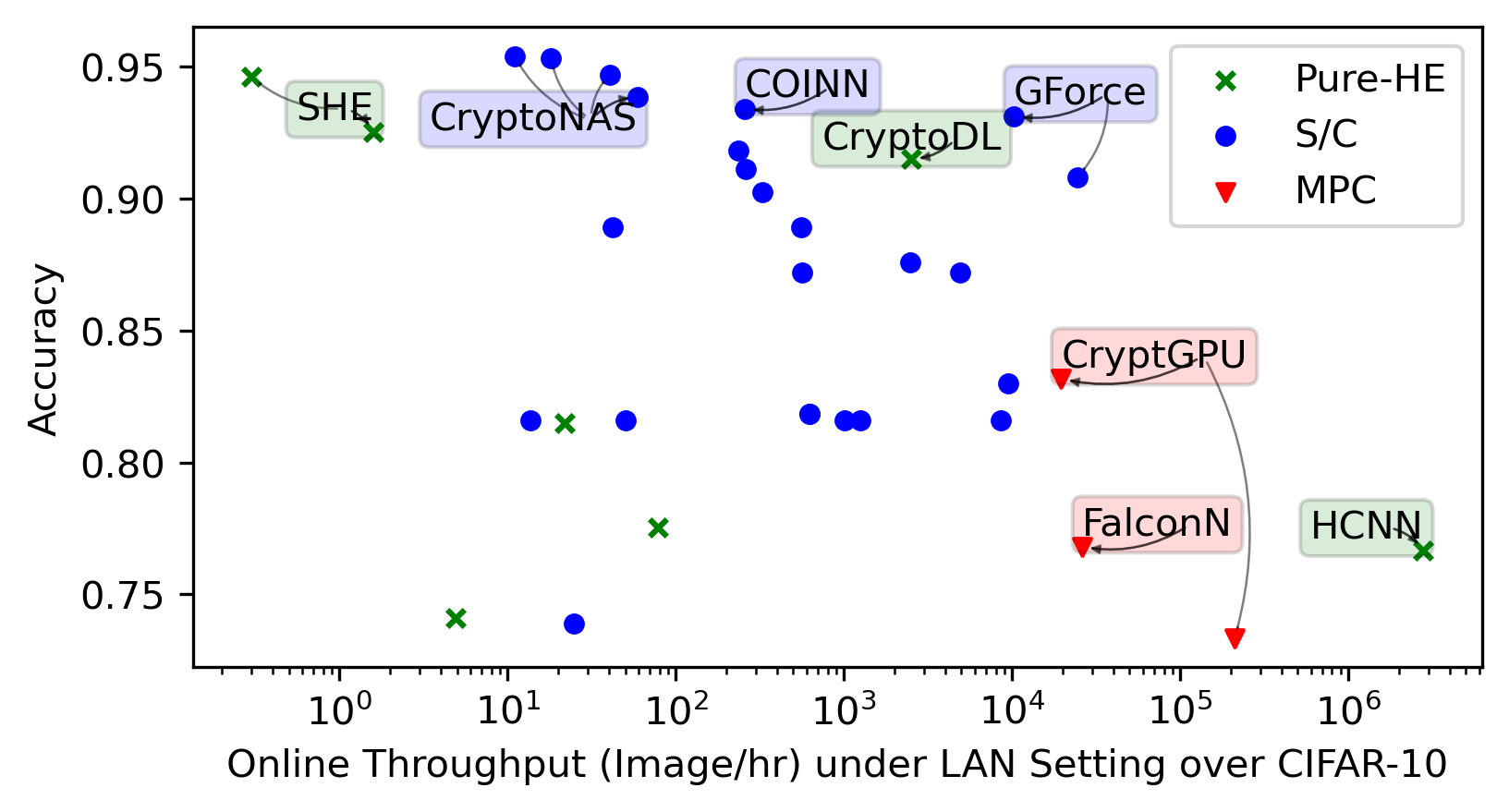

Figure 2: Online Throughput of Inference on CIFAR-10 (top-right ones are better)

Figure 2 shows that CryptGPU defeats GForce in throughput, probably for amortizing the communication cost between the \(3\) servers over its batched queries. CryptoDL (Hesamifard et al. 2018), using only LHE, achieves a throughput close to GForce (Ng and Chow 2021) and CryptGPU, the representative of the other approaches. It encodes all batched queries in an HE ciphertext to avoid expensive rotations.

For accuracy, circuit-based SHE (Lou and Jiang 2019) is the best, albeit the worst in throughput. Other pure-HE frameworks, e.g., CryptoDL, attain accuracy inferior to GForce and CryptGPU, the representative of the other \(2\) approaches. It shows that polynomial approximation bound to HE frameworks harms accuracy.

3. GPU Trumps. Figures for online latency and online throughput over CIFAR-10 show the important role of GPU. CryptGPU, GForce, and HCNN (Badawi et al. 2021) all utilize GPUs and achieve the shortest latency or the highest throughput among the frameworks of their respective major approach. We expect to see future frameworks will continue to involve GPUs.

Open Problem 11. What can other cryptographic primitives (for non-linear operations) be made GPU/TPU-friendly?

4. Re-evaluation over WAN.

The representative S/C and MPC frameworks are evaluated on LAN.

We re-evaluate GForce (Ng and Chow 2021) (for S/C), CryptGPU (Tan et al. 2021), FalconN (Wagh et al. 2021), and the Piranha (Watson, Wagh, and Popa 2022) version of FalconN on GPU (P-FalconN). (for MPC) to understand their performance under non-ideal network conditions. For LAN, they are state-of-the-art – GForce has the lowest latency, and all of them have (almost) the highest throughput. For Piranha, a GPU platform for MPC frameworks, we pick its instantiation for FalconN as it demonstrates the best performance among all existing instantiations.

The evaluation is done on a Google Cloud machine with \(4\) Nvidia V100 GPUs, an Intel Xeon 2.2GHz CPU with 32 cores, and \(64\)GB RAM. We set the communication latency to \(50\)ms because it is the latency for data centers communicating within a continent.

https://www.cloudping.co/grid

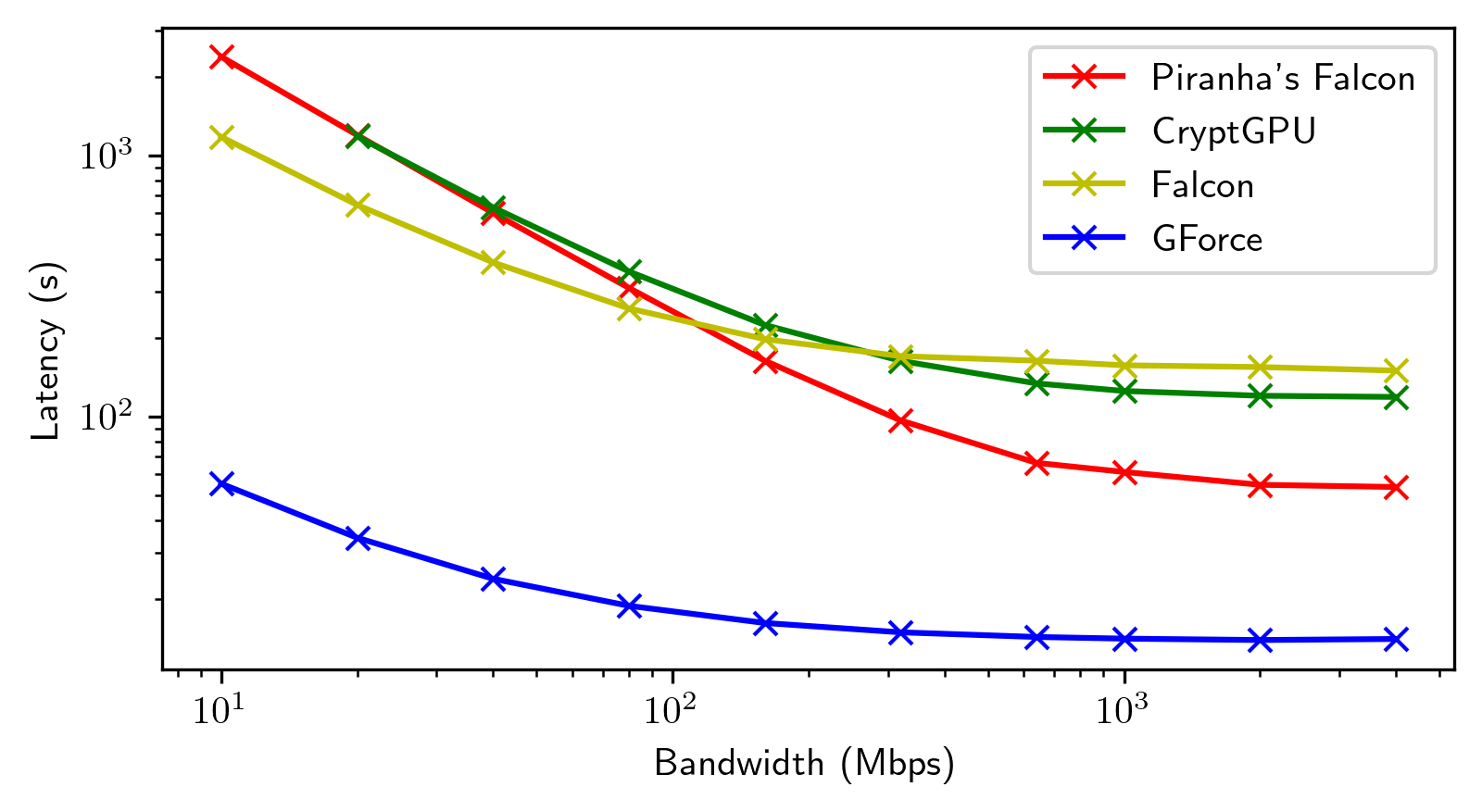
Figure 3: Our Re-evaluation for Latency over WAN (The lower the better)

Figure 3 shows their online latency in a WAN setting with \(50\)ms communication latency using the Linux \(\mathsf{tc}\) command for VGG-16 over CIFAR-10. GForce demonstrates the lowest latency, an order of magnitude lower than others. Its latency is \({\sim} 10\)s for \({\geq}100\)Mbps bandwidth and remains \({<}1\) minute even under \({\sim}10\)Mbps, which seems good enough for non-real-time usage. Notably, these frameworks still have shorter latency than the pure-HE frameworks in WAN. With only \(10{\sim}100\)Mbps, the re-evaluated MPC and S/C frameworks attain \(10^2{\sim}10^3\)s latency, which outperforms Faster-Crypt (with the shortest latency of \({\sim}10^5\)s among pure-HE frameworks in Figure 1.

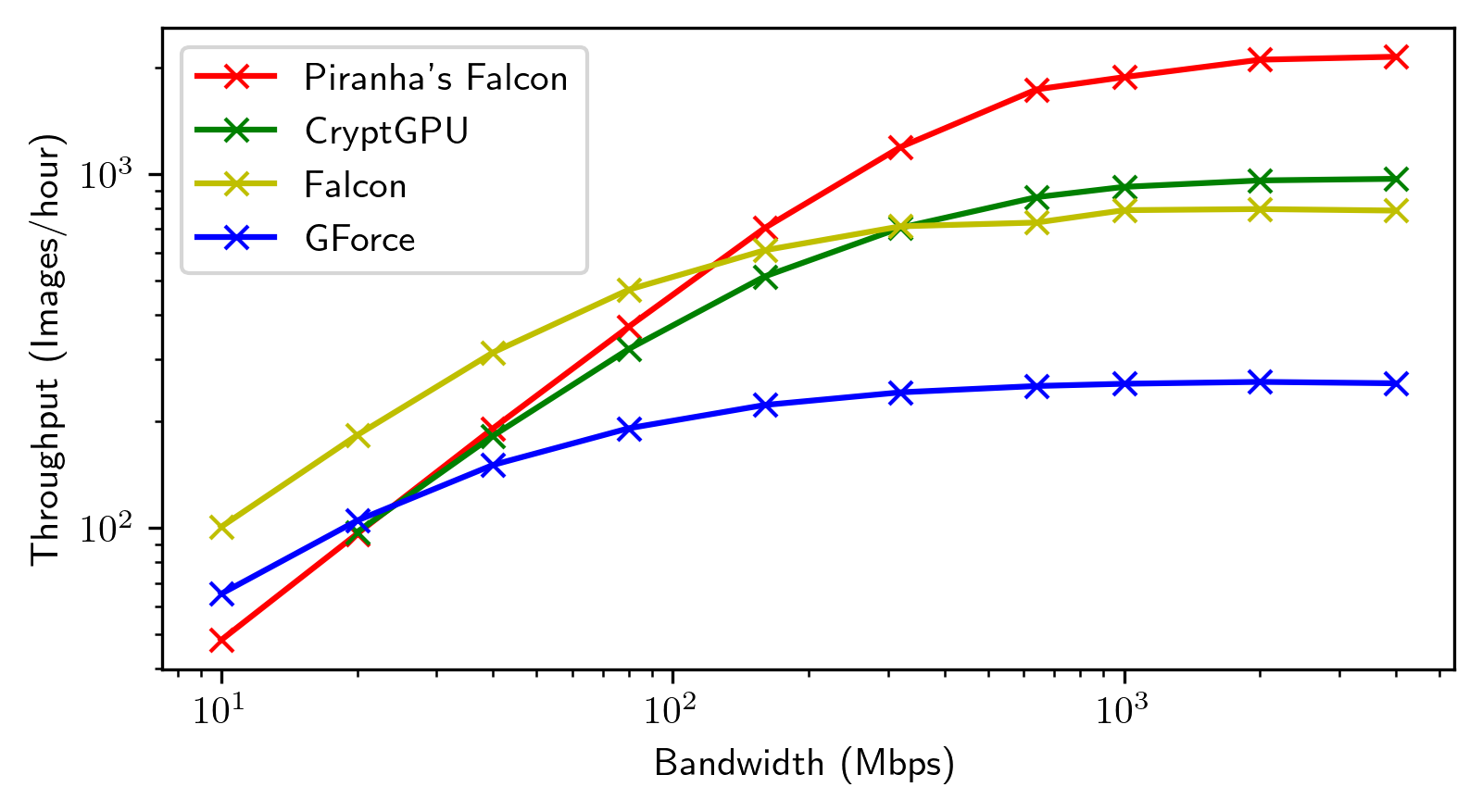
Figure 4: Our Re-evaluation for Throughput over WAN (The higher the better)

Figure 4 shows their online throughput under the same experimental setting. They show a decrease from the order of \(10^4\) images/hr in LAN to \(10^2{\sim}10^3\) in WAN. Similarly, their inference latency is increased by \(100\times\). When the bandwidth is high (\({\geq}100\)Mbps), their relative order remains similar to Figure 5. Compared to pure-HE frameworks, these MPC and S/C frameworks have lower throughput (\(10^2{\sim}10^3\) images/hr) than HCNN (\({\sim}10^4\) images/hr) and CryptoDL (\({>}10^3\) images/hr). It is expected because pure-HE is insensitive to network conditions and can leverage SIMD for higher throughput.

All frameworks appear to need \({\sim}1000\)Mbps to reach their peak performance. Notably, FalconN is less sensitive to low bandwidth as it starts to outperform Piranha and CryptGPU in extremely low bandwidth of \(10 \sim 100\)Mbps.

5. MNIST over WAN.

Pure-HE frameworks often perform the best in WAN settings for not requiring interaction and hence less affected by the communication latency. Yet, they support a limited depth of NNs and limited choices of non-linear layers, so they usually only handle MNIST, an easier dataset. We did not perform re-evaluations for MNIST being an unrealistically easy dataset to reflect performance for real tasks.

The definition of WAN varies across papers. Their network traffic latency ranges from \(40\) to \(150\)ms, and \(40\) to \(320\)Mbps for their bandwidth.

Figure 5 and 6 includes \(21\) frameworks:

• \(13\) pure-HE frameworks: CryptoNets (Gilad-Bachrach et al. 2016), CryptoDL (Hesamifard et al. 2018), E2DM (Jiang et al. 2018), Faster-Crypt (Chou et al. 2018), FHE-DiNN (Bourse et al. 2018), TAPAS (Sanyal et al. 2018), CHET (Dathathri et al. 2019), nGraph-HE (Boemer, Lao, et al. 2019), SEALion (Elsloo, Patrini, and Ivey-Law 2019), SHE (Lou and Jiang 2019) LoLa (Brutzkus, Gilad-Bachrach, and Elisha 2019), Glyph (Lou et al. 2020), and HCNN (Badawi et al. 2021).

• \(7\) MPC frameworks: FalconN (Wagh et al. 2021), Quotient (Agrawal et al. 2019), Blaze (Patra and Suresh 2020), SecureNN (Wagh, Gupta, and Chandran 2019), Trident (Rachuri and Suresh 2020), SecureML (Mohassel and Zhang 2017), and ABY3 (Mohassel and Rindal 2018).

• \(5\) outliers, namely, ABY3, FHE-DiNN, SecureML, Trident, and SecureNN, are omitted as their accuracy is only \({\sim}93\%\).

EzPC (Chandran et al. 2019) is the only S/C framework included since most S/C frameworks skip their WAN evaluation.

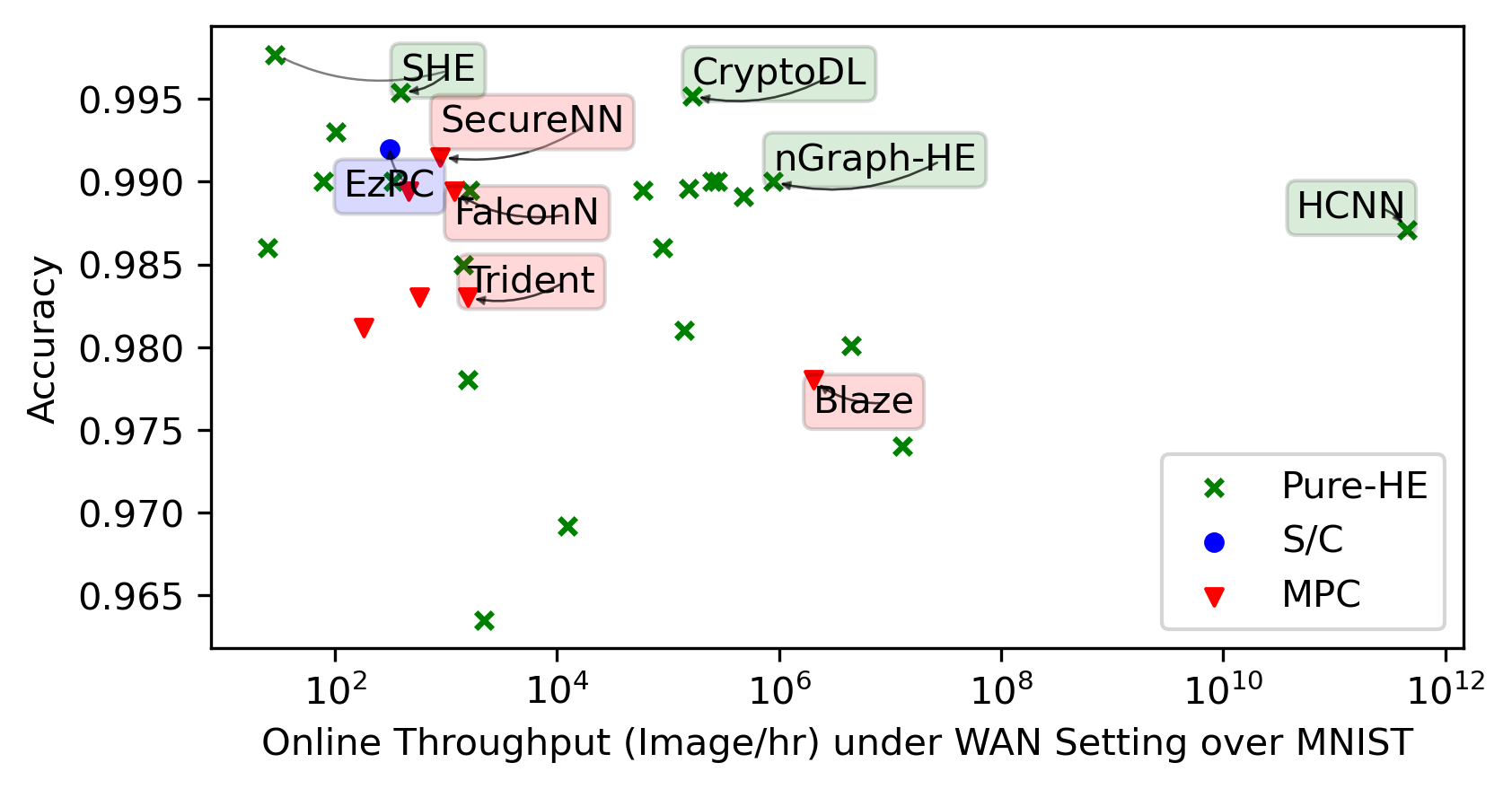
Figure 5: Online Throughput of Inference on MNIST (top-right ones are better

Figure 5 shows their online throughput in WAN. HCNN (using \(4\) GPUs) has the highest throughput. CryptoDL and nGraph-HE also strike a good balance between accuracy and throughput. These three frameworks use HE’s SIMD for batch processing. SecureNN, FalconN, Trident, and Blaze

are the Pareto frontiers of the MPC frameworks. Yet, they are all inferior to the frontiers of the pure-HE frameworks as they require more interactions.

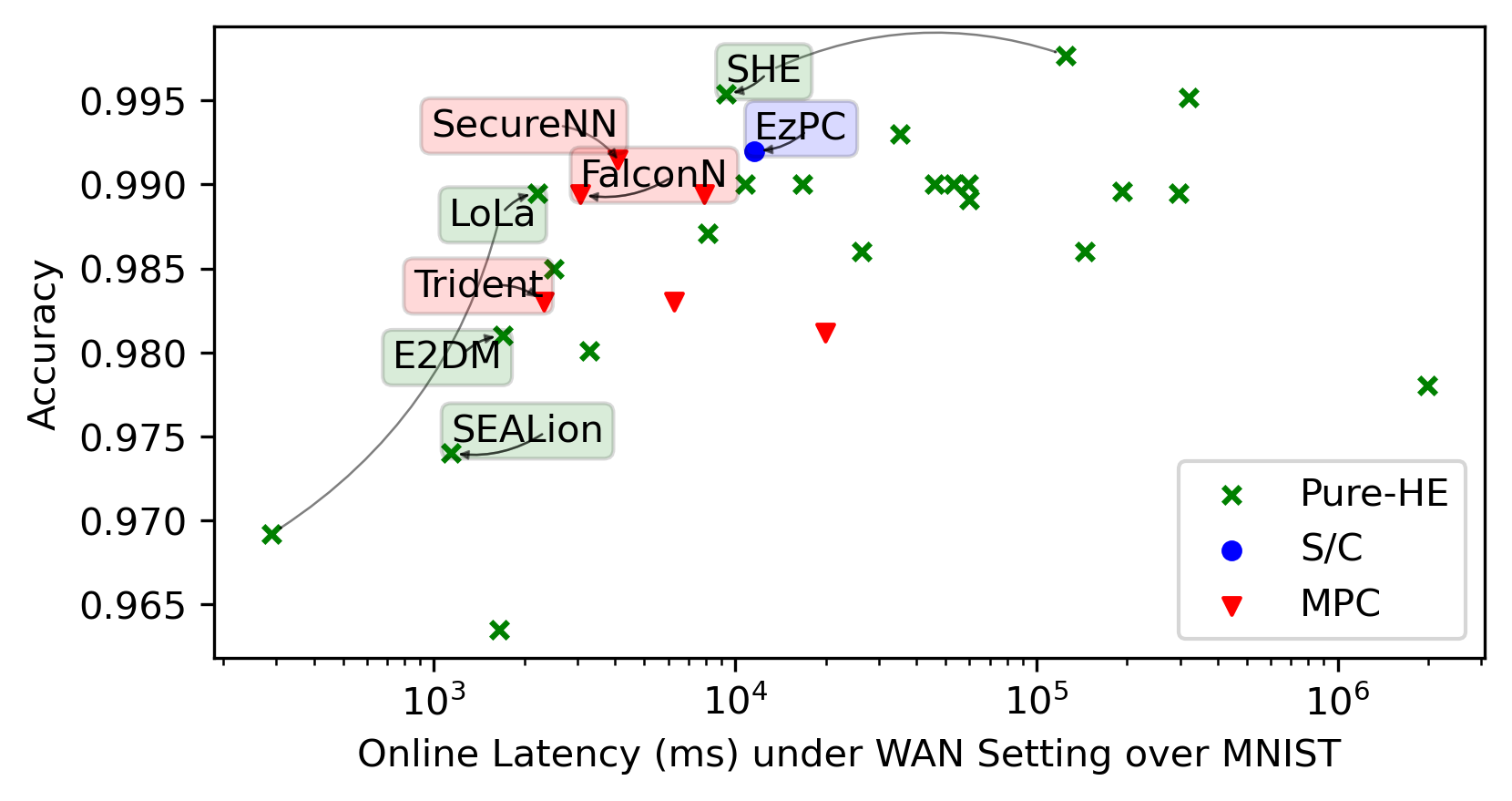
Figure 6: Online Latency of Inference on MNIST (top-left ones are better)

For online latency, LoLa reduces the rotation cost of SIMD, and Figure 6 shows its good balance with accuracy.

In general, pure-HE remains better than MPC, but their gap is much narrower since SIMD does not help as much. (SecureNN is also on the Pareto frontier for \(130\)ms latency. Yet, it is omitted from Figure 6 due to its low accuracy (\(93.4\%\)).)

Private Training

Among the \(9\) frameworks for private (and outsourced) training, CryptGPU (Tan et al. 2021), FalconN (Wagh et al. 2021), Piranha (Watson, Wagh, and Popa 2022), and AdamInPrivate (Attrapadung et al. 2022) are the only fours tested on CIFAR-10 or any harder datasets using deep NNs (VGG-16).

Table 3: REPORTED ACCURACY AND THROUGHPUT ON LAN

Training Framework	Accuracy	Throughput (Image/hr)
FalconN	76.8%	1482
Accuracy	82.3%	9489
P-FalconN	55.1%	15152
AdamInPrivate	75%	4171

As shown in Table 3, CryptGPU has the highest accuracy of \(82.3\%\), while P-FalconN (Piranha’s instantiation on FalconN) has the highest throughput. Yet, CryptGPU may still be the winner since accuracy is usually more important in NN training, when CryptGPU’s throughput (\(9489\) images/hr) is only slightly lower than P-FalconN’s (\(15152\) images/hr).

We note that frameworks for oblivious inference can attain \({>}90\%\) accuracy with the same architecture (VGG-16) adopted by CryptGPU. It implies the potential for improvements.

Challenge 15. How to attain a higher level of accuracy in private training? For instance, what other (normalization) layers can we use with what other approximation approaches?

Discussion

We give some brief guidance on what PPNN frameworks to use. The threat models and performance are the main concerns. If the users trust some non-colluding servers, they can outsource the NN computation for the best-in-the-class performance since non-colluding MPC frameworks often feature efficient outsourced training and inference.

If the users do not trust non-colluding servers, they have two choices left: 1. For inference expecting nearly real-time results, e.g., facial recognition, they can run S/C frameworks, e.g., GForce (Ng and Chow 2021), with a reasonably good network (\(\leq 50\)ms network latency and \(\geq 100\)Mbps) and using pre-computation to save online inference latency. 1. For applications that can wait or involve many sub-queries, e.g., medical diagnosis and financial data analysis. These applications can use pure-HE frameworks, e.g., CryptoDL, to achieve high throughput (but high inference latency) using SIMD, i.e., running the queries in batches.

Without non-colluding servers, E2DM and GarbledNN support outsourced inference, and Glyph supports outsourced training. Yet, their performance is far from the S/C and pure-HE frameworks. For detailed discussions about the state-of-the-art frameworks in different settings, see the Section on SoTA and Fig. 7.

We end with remarks on two popular application areas. Natural language processing often runs on RNNs, which require heavy computation due to recurrent calls to some gigantic NN that contains complex non-linear functions. SiRnn (Rathee et al. 2021) is the only efficient (non-colluding) framework for oblivious inference.

CryptGPU, FalconN, and AdamInPrivate, being non-colluding frameworks, also support those complex non-linear functions and thus should be able to train and infer over RNNs.

Graph NNs, which apply NNs for graphs, can use the techniques in this SoK in oblivious settings. Yet, it poses new challenges on how to hide the topology of the graphs.

The State of the Art for Various Setups/Features

Figure 7: The State of the Art with Different Features/Setups

This section shows which framework best fits a given scenario. Figure 7 serves as a decision tree guiding the choice.

Oblivious Inference without Non-colluding Servers

Figure 1 shows the accuracy and latency in a LAN setting of \({>}1\)Gbps and \({<}5\)ms communication latency.

Low-Latency Inference.

COINN (Hussain et al. 2021) and GForce (Ng and Chow 2021) are on the Pareto frontier, i.e., not superseded by any other in both accuracy and latency. Also, their latency is low (\(0.01{\sim}1\)s) for real-time usage.

Note that the servers and the clients may need offline preparation before the queries arrive.

High-Throughput Inference.

Online throughput shows the volume of queries answered in a given time. GForce still demonstrates high throughput, and COINN has its superiority in its high accuracy. HCNN (Badawi et al. 2021) exploits parallelism to achieve the highest throughput but attains relatively low accuracy (\(80\%\)).

Oblivious Inference under Nonideal Network Conditions.

Oblivious inference may go under a WAN (vs. the “ideal” LAN) setting, i.e., \({<}320\) Mbps and \({>}40\)ms latency. If large NNs for complex tasks and accuracy are paramount, S/C frameworks still seem to be the best, e.g., GForce (Ng and Chow 2021) still performs an inference within one minute, as shown in Figure 3.

For smaller NNs and easier tasks, e.g., MNIST, pure-HE frameworks perform better for their constant communication round. For throughput, CryptoDL (Hesamifard et al. 2018), nGraph-HE (Boemer, Lao, et al. 2019), and HCNN (Badawi et al. 2021) haVE the highest throughput and accuracy, as shown in Figure 5. For latency, LoLa (Brutzkus, Gilad-Bachrach, and Elisha 2019), E2DM (Jiang et al. 2018), and SEALion (Elsloo, Patrini, and Ivey-Law 2019) are on the Pareto frontier in Figure 6.

Outsourced Training/Inference.

Glyph (Lou et al. 2020) is the only option for outsourced training (but not private training). It also supports outsourced inference, but E2DM (Jiang et al. 2018) has better performance for using LHE and does not leak the weights of the first few layers to the client like Glyph.

Do Non-colluding-based Frameworks Always Win?

For oblivious inference, Figure 1 shows that GForce has the lowest latency, outperforming non-colluding frameworks. CryptGPU strikes the best balance of throughput and accuracy. Only Glyph can support secure training without non-colluding servers. Note that it requires public datasets for transfer training.

Non-colluding MPC Settings

\(2\) Non-colluding Servers.

SecureML and Quotient (Agrawal et al. 2019) are the only two. (ABY2.0 does not provide accuracy.) Quotient is reported to produce NNs with \(6\)pp higher accuracy on MNIST and \({>}5\times\)/\(50\times\) training throughput in the LAN/WAN setting.

\(3\) Non-colluding Servers.

CryptGPU (Tan et al. 2021) reports the highest accuracy, lower latency, and higher throughput than FalconN, SecureNN, and CrypTen in CIFAR-10. Yet, its throughput and latency are slightly worse than Piranha (Watson, Wagh, and Popa 2022), as discussed in the Section on benchmark.

Other \(3\)PC solutions (e.g., Blaze (Patra and Suresh 2020) and Swift (Koti et al. 2021)) only support inference and are tested on MNIST but not harder datasets. We remark that some of them can defend against malicious adversaries.

\(4\) Non-colluding Servers.

Fantastic Four (Dalskov, Escudero, and Keller 2021) reports that it has slightly better performance than Swift (Koti et al. 2021) and Flash (Byali et al. 2020). How it (Dalskov, Escudero, and Keller 2021) compared to Trident (Rachuri and Suresh 2020) is not clear because they have not compared themselves with each other but just emphasized their speed-up over ABY3 (Mohassel and Rindal 2018) as a reference point. Notably, they do not provide their training or inference accuracy over CIFAR-10.

Defending against Malicious Adversaries

A recent pursuit is to ensure security even when one server deviates from the protocol (but it still cannot collude with other servers) by fully exploiting non-colluding assumptions.

In the basic malicious setting (ABY3 (Mohassel and Rindal 2018), SecureNN (Wagh, Gupta, and Chandran 2019), and FalconN (Wagh et al. 2021)), honest servers would abort

if a corrupt server deviates from the protocol. For fairness (Malicious Security in our Summary of all Frameworks), all honest parties can get the output (of internal protocols) if the corrupted can receive it (Blaze (Patra and Suresh 2020) and Trident (Rachuri and Suresh 2020)), even if the corrupted is malicious (i.e., guarantee of delivery (G.O.D.) of Flash (Byali et al. 2020) and Swift (Koti et al. 2021)).

Muse (Lehmkuhl et al. 2021) features “abort security” against clients with higher efficiency than pure-GC approaches (Riazi et al. 2019; Ball et al. 2019).

Genealogy

Figure 8: The Genealogy of Frameworks (Names we came up with: BNormCrypt, GarbledNN, and FalconI/N for Inference/Training)

Summary of Frameworks

Interactive Chart

The following chart shows the accuracy and throughput/latency under various setting. You can scroll to zoom in or out the chart. You may use the drop-down lists to change the setting.

• For throughput, the closer to the top-right the better.
• For latency, the closer to the top-left the better.